The tram in Berland goes along a straight line from the point 0 to the point s and back, passing 1 meter per t1 seconds in both directions. It means that the tram is always in the state of uniform rectilinear motion, instantly turning around at points x?=?0 and x?=?s.
Igor is at the point x1. He should reach the point x2. Igor passes 1 meter per t2 seconds.
Your task is to determine the minimum time Igor needs to get from the point x1 to the point x2, if it is known where the tram is and in what direction it goes at the moment Igor comes to the point x1.
Igor can enter the tram unlimited number of times at any moment when his and the tram's positions coincide. It is not obligatory that points in which Igor enter and exit the tram are integers. Assume that any boarding and unboarding happens instantly. Igor can move arbitrary along the line (but not faster than 1 meter per t2 seconds). He can also stand at some point for some time.
The first line contains three integers s, x1 and x2 (2?≤?s?≤?1000, 0?≤?x1,?x2?≤?s, x1?≠?x2) — the maximum coordinate of the point to which the tram goes, the point Igor is at, and the point he should come to.
The second line contains two integers t1 and t2 (1?≤?t1,?t2?≤?1000) — the time in seconds in which the tram passes 1 meter and the time in seconds in which Igor passes 1 meter.
The third line contains two integers p and d (1?≤?p?≤?s?-?1, d is
either 1 or 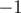 ) —
the position of the tram in the moment Igor came to the point x1 and
the direction of the tram at this moment. If
) —
the position of the tram in the moment Igor came to the point x1 and
the direction of the tram at this moment. If 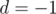 ,
the tram goes in the direction from the point s to the point 0.
Ifd?=?1, the tram goes in the direction from the point 0 to
the point s.
,
the tram goes in the direction from the point s to the point 0.
Ifd?=?1, the tram goes in the direction from the point 0 to
the point s.
Print the minimum time in seconds which Igor needs to get from the point x1 to the point x2.
4 2 4 3 4 1 1
8
5 4 0 1 2 3 1
7
In the first example it is profitable for Igor to go by foot and not to wait the tram. Thus, he has to pass 2 meters and it takes 8 seconds in total, because he passes 1 meter per 4 seconds.
In the second example Igor can, for example, go towards the point x2 and get to the point 1 in 6 seconds (because he has to pass 3meters, but he passes 1 meters per 2 seconds). At that moment the tram will be at the point 1, so Igor can enter the tram and pass 1meter in 1 second. Thus, Igor will reach the point x2 in 7 seconds in total.
Source
Codeforces Round #386 (Div. 2)
My Solution
題意:從x1 動身到 x2,走路速度是t2 s/ 單位長度 ,坐車是t1 s/ 單位長度,車子在0~s間不斷來回,此時車在p位置,且方向是d,(正向 d == 1,反向 d == ⑴) 問從x1到x2的最短時間
數學、討論
另外題可以分成2大類,到達的時候是走路的則只斟酌全走路,如果到達的時候是坐車則只斟酌坐車,
即x1到達x2所花的時間為此時p位置到最后以x1指向x2的方向經過x2時的總時間。
具體分成以下6類討論
當 x1 < x2 時
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
const int maxn = 1e6 + 8;
int main()
{
#ifdef LOCAL
freopen("c.txt", "r", stdin);
//freopen("c.out", "w", stdout);
int T = 4;
while(T--){
#endif // LOCAL
ios::sync_with_stdio(false); cin.tie(0);
LL s, x1, x2, t1, t2, p, d, ans = 9e18;
cin >> s >> x1 >> x2;
cin >> t1 >> t2;
cin >> p >> d;
if(x1 < x2){
ans = (x2 - x1) * t2;
if(d == 1){
if(p <= x1){
ans = min(ans, (x2 - p) * t1);
}
else{
ans = min(ans, (s + x2 + s - p) * t1);
}
}
else{
ans = min(ans, (p + x2) * t1);
}
}
else{
ans = (x1 - x2) * t2;
if(d == 1){
ans = min(ans, (s - p + s - x2) * t1); //(©D£?©D)
}
else{
if(p >= x1){
ans = min(ans, (p - x2) * t1);
}
else{
ans = min(ans, (p + s + s - x2) * t1);
}
}
}
cout << ans << endl;
#ifdef LOCAL
cout << endl;
}
#endif ** LOCAL
return 0;
}
Thank you!
------from ProLights
