Codeforces Round #385 (Div. 2) C. Hongcow Builds A Nation 并查集+貪心+組合學、圖論、dfs

4 1 2
1 3
1 2

2

3 3 1
2
1 2
1 3
2 3

0

Note

For the first sample test, the graph looks like this:

Vertices 1 and 3 are special. The optimal solution is to connect vertex 4 to vertices 1 and 2. This adds a total of 2 edges. We cannot add any more edges, since vertices 1 and 3 cannot have any path between them.

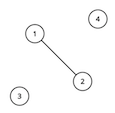
For the second sample test, the graph looks like this:

We cannot add any more edges to this graph. Note that we are not allowed to add self-loops, and the graph must be simple.

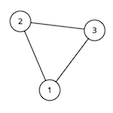
Source

Codeforces Round #385 (Div. 2)

My Solution

題意：有n個點(其中有k個關鍵點)，m條邊，要求添加盡量多的邊使得k個關鍵點之間沒有路徑，問最多可以添加多少條邊。

并查集+貪心+組合學、圖論、dfs

用并查集處理這個圖，相干聯的點構成1顆樹，然后把每棵樹的結點數貯存在該樹的根節點上，

然后開始貪心，找出k個關鍵點里，關鍵點所在樹的結點個數最多的結點 maxci，

然后把這個ci 和它所關聯的點 與 所有無關鍵點出現的樹相結合(free)，構成1個連通塊，這個連通塊的總邊數是 (free + maxcnt) * (free + maxcnt - 1) / 2;

然后剩下的是除這個maxci以外的有關鍵點的樹，這些樹貯存的點構成完全圖的邊數是 if(i != maxci)  ans += cnt[_find(c[i])] * (cnt[_find(c[i])] - 1) / 2;

所有得到的ans 是滿足條件時的圖的總邊數，減點輸入的m條邊， ans - m 即為在公道的情況下可以添加的最大邊數

復雜度 O(n^2)

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const int maxn = 1e3 + 8;

//有時可能需要 并查集+離散化
int father[maxn], _rank[maxn];
inline void DisjointSet(int n)
{
    for(int i = 0; i <= n; i++){
        father[i] = i;
    }
}

inline int _find(int v)
{
    return father[v] = father[v] == v ? v : _find(father[v]);
    //同時緊縮路徑，有時不能緊縮路徑，有時必須緊縮路徑，看具體情況
}

inline void _merge(int x, int y)
{
    int a = _find(x), b = _find(y);                //
    if(_rank[a] < _rank[b]){
        father[a] = b;
    }
    else{
        father[b] = a;
        if(_rank[a] == _rank[b]){
            _rank[a]++;
        }
    }
}

LL c[maxn], cnt[maxn], maxci;
bool flag[maxn];
int main()
{
    #ifdef LOCAL
    freopen("d.txt", "r", stdin);
    //freopen("d.out", "w", stdout);
    int T = 4;
    while(T--){
    #endif // LOCAL
    ios::sync_with_stdio(false); cin.tie(0);

    int n, m, k, u, v;
    cin >> n >> m >> k;
    for(int i = 0; i < k; i++){
        cin >> c[i];
    }
    DisjointSet(n);
    for(int i = 0; i < m; i++){
        cin >> u >> v;
        if(_find(u) != _find(v)) _merge(u, v);
    }

    for(int i = 1; i <= n; i++){
        cnt[_find(i)]++;
    }
    LL maxcnt = 0;
    for(int i = 0; i < k; i++){
        if(maxcnt < cnt[_find(c[i])]){
            maxcnt = cnt[_find(c[i])];
            maxci = i;
        }
        flag[_find(c[i])] = true;
    }
    LL free = 0;
    for(int i = 1; i <= n; i++){
        if(!flag[i]){
            free += cnt[i];
        }
    }

    LL ans = (free + maxcnt) * (free + maxcnt - 1) / 2;
    for(int i = 0; i < k; i++){
        if(i != maxci){
            ans += cnt[_find(c[i])] * (cnt[_find(c[i])] - 1) / 2;
        }
    }

    cout << ans - m << endl;

    #ifdef LOCAL
    memset(flag, false, sizeof flag);
    memset(cnt, 0, sizeof cnt);
    cout << endl;
    }
    #endif // LOCAL
    return 0;
}

  Thank you!

                                                                                                                                               ------from ProLights

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈