Santa Claus has Robot which lives on the infinite grid and can move along its lines. He can also, having a sequence of m pointsp1,?p2,?...,?pm with integer coordinates, do the following: denote its initial location by p0. First, the robot will move from p0 to p1 along one of the shortest paths between them (please notice that since the robot moves only along the grid lines, there can be several shortest paths). Then, after it reaches p1, it'll move to p2, again, choosing one of the shortest ways, then to p3, and so on, until he has visited all points in the given order. Some of the points in the sequence may coincide, in that case Robot will visit that point several times according to the sequence order.
While Santa was away, someone gave a sequence of points to Robot. This sequence is now lost, but Robot saved the protocol of its unit movements. Please, find the minimum possible length of the sequence.
The first line of input contains the only positive integer n (1?≤?n?≤?2·105) which equals the number of unit segments the robot traveled. The second line contains the movements protocol, which consists of n letters, each being equal either L, or R, or U, or D. k-th letter stands for the direction which Robot traveled the k-th unit segment in: L means that it moved to the left, R — to the right, U — to the top and D — to the bottom. Have a look at the illustrations for better explanation.
The only line of input should contain the minimum possible length of the sequence.
4 RURD
2
6 RRULDD
2
26 RRRULURURUULULLLDLDDRDRDLD
7
3 RLL
2
4 LRLR
4
The illustrations to the first three tests are given below.
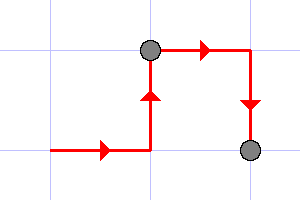
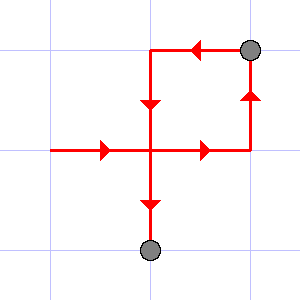
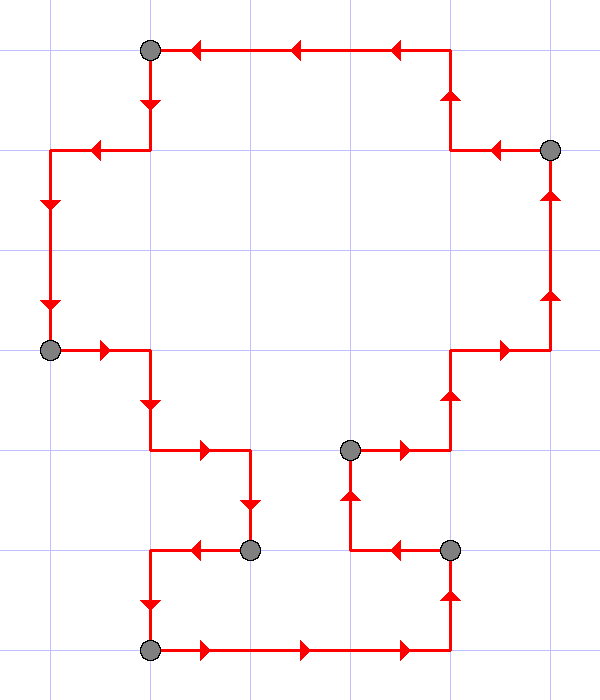
The last example illustrates that each point in the sequence should be counted as many times as it is presented in the sequence.
Source
Codeforces Round #389 (Div. 2, Rated, Based on Technocup 2017 - Elimination Round 3)
My Solution
題意:給定1個路徑,讓找出盡量少的關鍵點,沒相鄰的2個關鍵點的路徑必須是最短路徑
貪心+最短路
這是1個很有趣的題 Y ^_^ Y
ans = 0;
(px,py)表示最近出現的1個關鍵點坐標,cnt表示從最近的那個關鍵點到當前點所走的路程, (x, y)表示當前所在的點的坐標。
然后每步更新cnt及(x, y)后 判斷abs(px - x) + abs(py - y) == cnt,如果成立則從最近的1個關鍵點到當前點1直在根據最短路走,直到每次出現不公道的情況,則上1個點更新為新的最近的關鍵點,并且ans++,掃1遍,最后1個點必定是關鍵點,故額外 ans++ 把最后1個點加上。
復雜度 O(n)
#include <iostream>
#include <cstdio>
#include <string>
#include <cmath>
using namespace std;
typedef long long LL;
const int maxn = 1e6 + 8;
string s;
int main()
{
#ifdef LOCAL
freopen("c.txt", "r", stdin);
//freopen("c.out", "w", stdout);
int T = 8;
while(T--){
#endif // LOCAL
ios::sync_with_stdio(false); cin.tie(0);
int n, px = 0, py = 0, x = 0, y = 0, rx = 0, ry = 0, ans = 0, cnt = 0;
cin >> n;
cin >> s;
bool flag = false;
for(int i = 0; i < n; i++){
rx = x, ry = y;
if(s[i] == 'L'){
x--;
}
else if(s[i] == 'R'){
x++;
}
else if(s[i] == 'U'){
y++;
}
else if(s[i] == 'D'){
y--;
}
cnt++;
if(abs(px - x) + abs(py - y) == cnt){
//if(!flag){ans++; flag = true; }
}
else{
ans++;
//if(flag) ans++;
cnt = 1;
px = rx;
py = ry;
//cout << px << ' ' << py << endl;
}
}
ans++;
cout << ans << endl;
#ifdef LOCAL
cout << endl;
}
#endif // LOCAL
return 0;
}
Thank you!
------from ProLights
