1. 快速排序

介紹：

快速排序是由東尼·霍爾所發(fā)展的1種排序算法。在平均狀態(tài)下，排序 n 個項目要Ο(n log n)次比較。在最壞狀態(tài)下則需要Ο(n2)次比較，但這類狀態(tài)其實不常見。事實上，快速排序通常明顯比其他Ο(n log n) 算法更快，由于它的內(nèi)部循環(huán)（inner loop）可以在大部份的架構(gòu)上很有效力地被實現(xiàn)出來，且在大部份真實世界的數(shù)據(jù)，可以決定設(shè)計的選擇，減少所需時間的2次方項之可能性。

步驟：

從數(shù)列中挑出1個元素，稱為 “基準(zhǔn)”（pivot），
重新排序數(shù)列，所有元素比基準(zhǔn)值小的擺放在基準(zhǔn)前面，所有元素比基準(zhǔn)值大的擺在基準(zhǔn)的后面（相同的數(shù)可以到任1邊）。在這個分區(qū)退出以后，該基準(zhǔn)就處于數(shù)列的中間位置。這個稱為分區(qū)（partition）操作。
遞歸地（recursive）把小于基準(zhǔn)值元素的子數(shù)列和大于基準(zhǔn)值元素的子數(shù)列排序。

排序效果：

2. 歸并排序

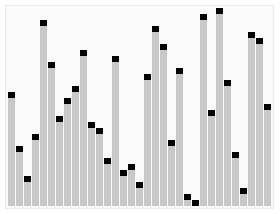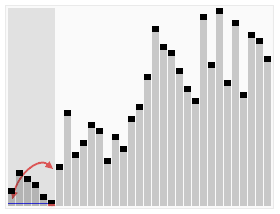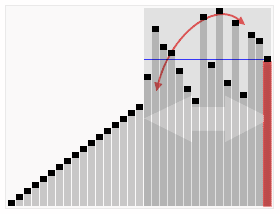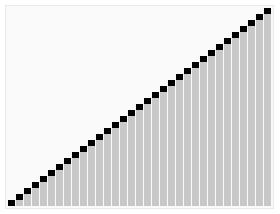
介紹：

歸并排序（Merge sort，臺灣譯作：合并排序）是建立在歸并操作上的1種有效的排序算法。該算法是采取分治法（Divide and Conquer）的1個非常典型的利用

步驟：

申請空間，使其大小為兩個已排序序列之和，該空間用來寄存合并后的序列
設(shè)定兩個指針，最初位置分別為兩個已排序序列的起始位置
比較兩個指針?biāo)赶虻脑兀x擇相對小的元素放入到合并空間，并移動指針到下1位置
重復(fù)步驟3直到某1指針到達序列尾
將另外一序列剩下的所有元素直接復(fù)制到合并序列尾

排序效果：

3. 堆排序

介紹：

堆積排序（Heapsort）是指利用堆這類數(shù)據(jù)結(jié)構(gòu)所設(shè)計的1種排序算法。堆是1個近似完全2叉樹的結(jié)構(gòu)，并同時滿足堆性質(zhì)：即子結(jié)點的鍵值或索引總是小于（或大于）它的父節(jié)點。

步驟：

（比較復(fù)雜，自己上網(wǎng)查吧）

排序效果：

4. 選擇排序

介紹：

選擇排序(Selection sort)是1種簡單直觀的排序算法。它的工作原理以下。首先在未排序序列中找到最小元素，寄存到排序序列的起始位置，然后，再從剩余未排序元素中繼續(xù)尋覓最小元素，然后放到排序序列末尾。以此類推，直到所有元素均排序終了。

排序效果：

5. 冒泡排序

介紹：

冒泡排序（Bubble Sort，臺灣譯為：泡沫排序或氣泡排序）是1種簡單的排序算法。它重復(fù)地訪問過要排序的數(shù)列，1次比較兩個元素，如果他們的順序毛病就把他們交換過來。訪問數(shù)列的工作是重復(fù)地進行直到?jīng)]有再需要交換，也就是說該數(shù)列已排序完成。這個算法的名字由來是由于越小的元素會經(jīng)過交換漸漸“浮”到數(shù)列的頂端。

步驟：

比較相鄰的元素。如果第1個比第2個大，就交換他們兩個。
對每對相鄰元素作一樣的工作，從開始第1對到結(jié)尾的最后1對。在這1點，最后的元素應(yīng)當(dāng)會是最大的數(shù)。
針對所有的元素重復(fù)以上的步驟，除最后1個。
延續(xù)每次對愈來愈少的元素重復(fù)上面的步驟，直到?jīng)]有任何1對數(shù)字需要比較。

排序效果：

6. 插入排序

介紹：

插入排序（Insertion Sort）的算法描寫是1種簡單直觀的排序算法。它的工作原理是通過構(gòu)建有序序列，對未排序數(shù)據(jù)，在已排序序列中從后向前掃描，找到相應(yīng)位置并插入。插入排序在實現(xiàn)上，通常采取in-place排序（即只需用到O(1)的額外空間的排序），因此在從后向前掃描進程中，需要反復(fù)把已排序元素逐漸向后挪位，為最新元素提供插入空間。

步驟：

從第1個元素開始，該元素可以認(rèn)為已被排序
取出下1個元素，在已排序的元素序列中從后向前掃描
如果該元素（已排序）大于新元素，將該元素移到下1位置
重復(fù)步驟3，直到找到已排序的元素小于或等于新元素的位置
將新元素插入到該位置中
重復(fù)步驟2

排序效果：

（暫無）

7. 希爾排序

介紹：

希爾排序，也稱遞減增量排序算法，是插入排序的1種高速而穩(wěn)定的改進版本。

希爾排序是基于插入排序的以下兩點性質(zhì)而提出改進方法的：

1、插入排序在對幾近已排好序的數(shù)據(jù)操作時， 效力高， 便可以到達線性排序的效力

2、但插入排序1般來講是低效的， 由于插入排序每次只能將數(shù)據(jù)移動1位>

排序效果：

回頭有時間把每種算法的代碼實現(xiàn)也給放上去就完善了，歡迎各位查找bug,提出自己的見解！