本文首先介紹了從傅里葉變換到小波變換的發(fā)展史,然后側(cè)重強調(diào)了小波變換的兩種作用——時頻分析和多分辨率分析,最后講了1下吉布斯效應等相干知識。
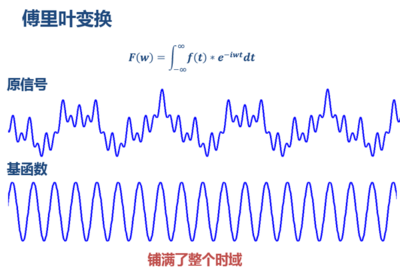
FT(傅里葉變換),通過將信號分解成正余弦函數(shù)(把3角函數(shù)當作函數(shù)空間的基),將時域信號轉(zhuǎn)化為頻域信號。缺點是只適用于安穩(wěn)性信號,在頻域圖上不能取得對應頻率的時間信息。

由上圖可以看到,對頻域成份相同的信號,即便信號在時域上的散布不1樣,F(xiàn)FT變換后的頻域圖卻幾近完全1樣。所以說,F(xiàn)FT只可以取得1段信號整體上包括哪些成份,但是對各成份出現(xiàn)的時間并沒有所知。因此時域相差很大的信號FFT以后的頻域圖可能完全相同。
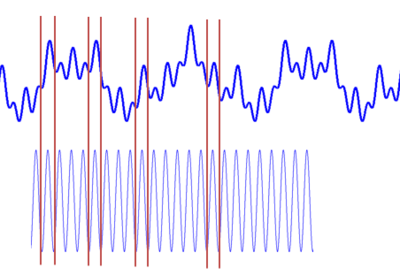
STFT(短時傅里葉變換)添加時域信息的方法是設(shè)置窗格,認為窗格內(nèi)的信號是安穩(wěn)信號,對窗格內(nèi)的信號分段進行FT分析。優(yōu)點是可以取得頻域信息的同時可以取得時域信息。缺點是窗格大小很難設(shè)置。
STFT的方法及效果以下圖:
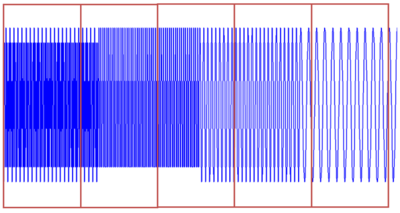
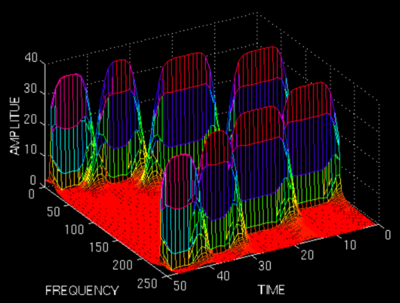
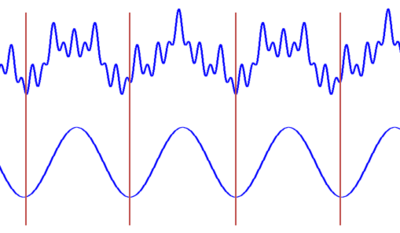
STFT的窗格問題以下:
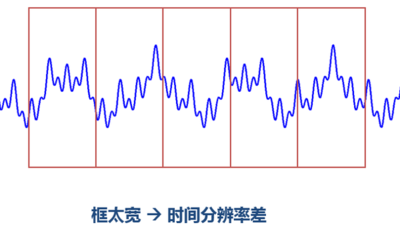
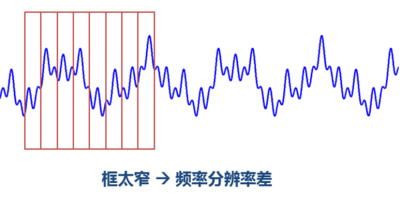
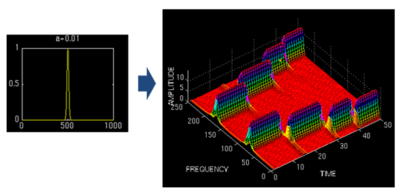
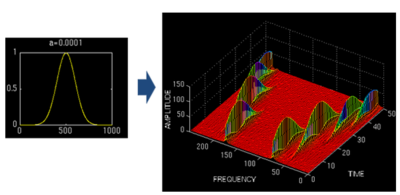
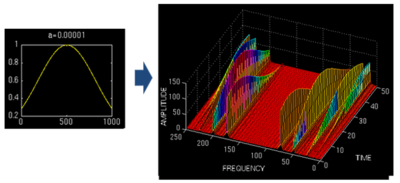
由上面的圖可以看到,窄窗口時間分辨率高、頻率分辨率低;寬窗口時間分辨率低,頻率分辨率高。對時變的非穩(wěn)態(tài)信號,高頻合適小窗口,低頻合適大窗口。可是STFT的窗口是固定的,因此需要尋求別的方法。
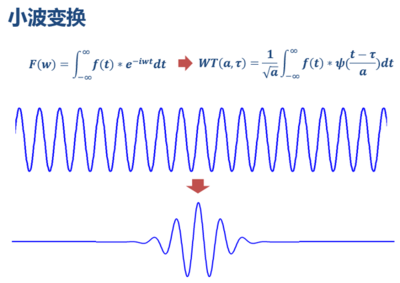
WT(小波變換),將傅里葉變換的基給換了—— 將無窮長的3角函數(shù)基換成了有限長的會衰減的小波基,這樣不但可以獲得頻率,還可以定位到時間。
傅里葉變換,通過相互正交的3角函數(shù)信號和原信號在無窮上進行積分,積分越大表明信號越類似,包括該頻率的3角信號也就越多。
最后,每個f值對應了1個積分值,取得了頻率圖。
小波變換的原理類似傅里葉變換,只是把3角函數(shù)基換成了小波基。
與傅里葉變換不同,小波變換有兩個變量:scale和translation。scale控制小波函數(shù)的收縮,其導數(shù)即為頻率,translation控制小標函數(shù)的平移,平移量對應時間。
通過信號的伸縮平移,可以得到某種重合情況,這樣積分也會得到1個極大值,不同的是,得到頻率成份的同時,還可以知道該頻率的時間位置。
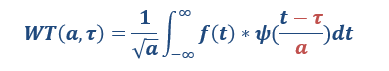
.png)
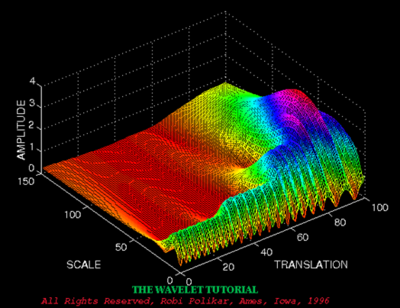
最后得到的也是3維的圖象:

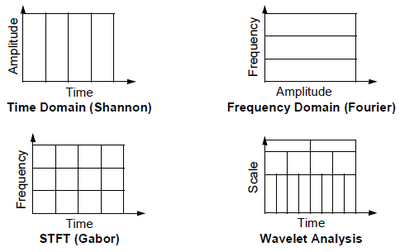
傅里葉變換,選擇正弦函數(shù)作為基函數(shù),然后考察的到的展開式的性質(zhì)。
對小波分析,首先提出想要的性質(zhì),然后推導出基函數(shù)。
小波的1個思想是在時間和頻率兩個方面提供有效的局部化,另外一個中心思想是多分辨率,即信號的分解是依照不同分辨率的細節(jié)1層1層進行的。
對2維函數(shù)族(構(gòu)成空間的基底):
對所有
如果
也就是說,
低分辨率上的信號,不但可以通過該低分辨率上的信號基底組合,還可以通太高分辨率上信號的基底組合起來。
尺度函數(shù)
如果您覺得本網(wǎng)站對您的學習有所幫助,可以手機掃描二維碼進行捐贈
