本系列文章都是關(guān)于UFLDL Tutorial的學(xué)習(xí)筆記

Neural Networks

• 對(duì)1個(gè)有監(jiān)督的學(xué)習(xí)問題，訓(xùn)練樣本輸入情勢(shì)為(x(i),y(i))。使用神經(jīng)網(wǎng)絡(luò)我們可以找到1個(gè)復(fù)雜的非線性的假定h(x(i))可以擬合我們的數(shù)據(jù)y(i)。我們先視察1個(gè)神經(jīng)元的機(jī)制：

  

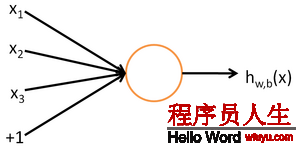
• 每一個(gè)神經(jīng)元是1個(gè)計(jì)算單元，輸入為x1,x2,x3，輸出為：

  

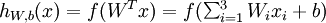
• 其中f()是激活函數(shù)，經(jīng)常使用的激活函數(shù)是S函數(shù)：

  

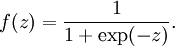
• S函數(shù)的形狀以下，它有1個(gè)很好的性質(zhì)就是導(dǎo)數(shù)很方便求：f’(z) = f(z)(1 ? f(z))：

  

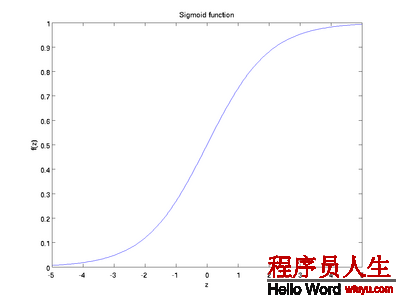
• 還有1個(gè)常見的激活函數(shù)是雙曲正切函數(shù)tanh:

  

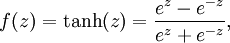
• 它的導(dǎo)數(shù)f’(z) = 1 ? (f(z))^2):

  

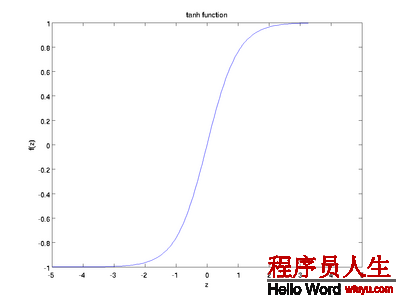
• softmax激活函數(shù)的導(dǎo)數(shù)：f’(z)=f(z)?f(z)^2

• S函數(shù)的取值在[0,1]之間，而tan函數(shù)的取值在[⑴,1]之間.

Neural Network model

• 神經(jīng)網(wǎng)絡(luò)就是將上面的單個(gè)神經(jīng)元連接成1個(gè)復(fù)雜的網(wǎng)絡(luò)：

  

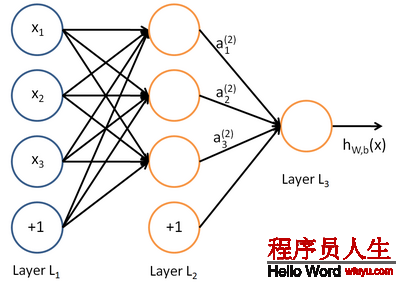
• 如圖所示的3層神經(jīng)網(wǎng)絡(luò)包括1個(gè)輸入層（3個(gè)輸入單元），1個(gè)隱藏層（3個(gè)計(jì)算單元），1個(gè)輸出層（1個(gè)輸出單元）。我們的所有參數(shù)描寫為(W,b) = (W(1),b(1),W(2),b(2))。Ws_ij表示的是第s層的第j個(gè)神經(jīng)元到第s+1層的第i個(gè)神經(jīng)元的權(quán)值，同理bs_i表示第s+1層的第i個(gè)神經(jīng)元的偏差。可知，偏差b的數(shù)目等于總的神經(jīng)元的個(gè)數(shù)減去輸入層的神經(jīng)元個(gè)數(shù)（輸入層不需要偏差），而權(quán)值w的數(shù)目等于神經(jīng)網(wǎng)絡(luò)的連接數(shù)。最后的輸出計(jì)算以下：

  

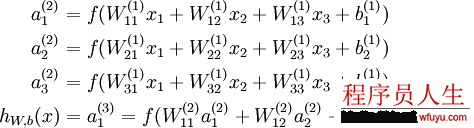
• 更緊湊的寫法就是講其寫成向量的積，這樣以矩陣的情勢(shì)存儲(chǔ)系數(shù)可以加速計(jì)算。其中z表示該層所有神經(jīng)元的輸入，a表示該層的輸出：

  

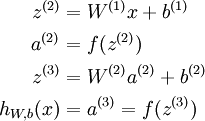
• 我們把上面這類求終究輸出的算法稱為向前傳播（feedforward）算法。對(duì)輸入層，我們可以用a1=x表示。給定l層的激活值al,計(jì)算l+1層的激活值的公式以下：

  

Backpropagation Algorithm

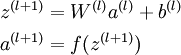
• 假定我們現(xiàn)在有1個(gè)固定大小為m的訓(xùn)練集{（x1,y1）,（x2,y2）…（xm,ym）}，我們使用批梯度降落法來訓(xùn)練我們的網(wǎng)絡(luò)。對(duì)每一個(gè)訓(xùn)練樣本（x,y），我們計(jì)算它的損失函數(shù)以下：

  

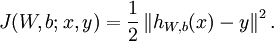
• 引入規(guī)范化（權(quán)重衰減項(xiàng)：weight decay），使得系數(shù)盡量的小，總的損失函數(shù)以下：

  

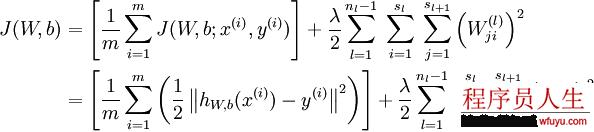
• 需要注意的是通常規(guī)范化不會(huì)使用在偏差b上，由于對(duì)b使用規(guī)范化終究取得網(wǎng)絡(luò)和之前沒有太大區(qū)分。這里的規(guī)范化實(shí)際上是貝葉斯規(guī)范化的1個(gè)變體，具體可以看CS229 (Machine Learning) at Stanford的視頻。

• 上面的損失函數(shù)通常在分類和回歸問題中被用到。在分類中通常y取值為0,1，而我們的S函數(shù)的取值范圍是在[0,1]之間。而如果使用tanh函數(shù)，由于取值范圍是[⑴,1]，我們可以將⑴表示0，1表示1，可以將0作為分界值。對(duì)回歸問題我們則需要先將我們的輸出按比例縮小到[0,1]之間，然后最后預(yù)測(cè)時(shí)相應(yīng)的放大。

• 我們的目標(biāo)是最小化損失函數(shù)J：首先隨機(jī)初始化w和b，由于梯度降落法容易局部最優(yōu)，因此要進(jìn)行屢次實(shí)驗(yàn)，每次隨機(jī)選擇的參數(shù)不能相同。計(jì)算完所有樣本的損失后，更新w和b的公式以下，其中α是學(xué)習(xí)率：

  

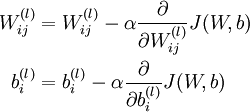
• 對(duì)這個(gè)更新公式，最核心的是計(jì)算偏導(dǎo)。我們采取反向傳播（ backpropagation）算法來計(jì)算偏導(dǎo)。反向傳播能夠幫助解釋網(wǎng)絡(luò)的權(quán)重和偏置的改變是如何改變代價(jià)函數(shù)的。歸根結(jié)柢，它的意思是指計(jì)算偏導(dǎo)數(shù)?C/?wl_jk和?C/?bl_j。但是為了計(jì)算這些偏導(dǎo)數(shù)，我們首先介紹1個(gè)中間量，δl_j，我們管它叫做第l層的第j個(gè)神經(jīng)元的毛病量(error)。我們可以先計(jì)算1個(gè)樣本產(chǎn)生的梯度向量，最后求所有樣本梯度的平均便可：

  

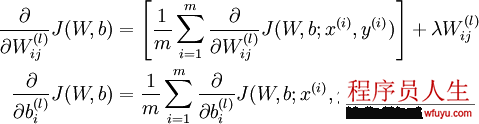
反向傳播具體推導(dǎo)以下：

1. 首先使用向前傳播計(jì)算出L2,L3…和輸出層的激活值。

2. 對(duì)輸出層的每個(gè)輸出單元計(jì)算毛病量（a=f(z)利用偏導(dǎo)的鏈?zhǔn)椒▌t）：

   

3. 對(duì)中間的隱藏層，我們計(jì)算每一個(gè)神經(jīng)元的毛病量。其中括號(hào)里面可以理解為l+1層所有與l層該神經(jīng)元相連的偏導(dǎo)乘以權(quán)值即為該神經(jīng)元的損失值：

   

4. 定義偏導(dǎo)以下：

   

• 訓(xùn)練神經(jīng)網(wǎng)絡(luò)的偽代碼以下（后面的λW是規(guī)范化項(xiàng)）：

根據(jù)neural networks and deep learning這本書中對(duì)反向傳播是這么理解的：

• 對(duì)第l層第j個(gè)神經(jīng)元，如果zl_j變成zl_j+Δzl_j，那末會(huì)對(duì)終究整體的損失帶來(?C/?zl_j)*Δzl_j的改變。反向傳播的目的是找到這個(gè)Δzl_j，使得終究的損失函數(shù)更小。假定?C/?zl_j的值很大（不論正負(fù)），我們期望找到1個(gè)和?C/?zl_j符號(hào)相反的Δzl_j使得損失下降。假定?C/?zl_j的值趨近于0，那末Δzl_j對(duì)損失的改變是微不足道的，表示這個(gè)神經(jīng)元和訓(xùn)練接近最優(yōu)了。這里以1個(gè)啟發(fā)式的感覺將?C/?zl_j看成度量1個(gè)神經(jīng)元的誤差的方法。

• 受上面的啟發(fā)，我們可以定義第l層第j個(gè)神經(jīng)元的誤差是：

  

• 輸出層誤差的方程，這個(gè)是根據(jù)偏導(dǎo)數(shù)鏈?zhǔn)椒▌t ?C/?z= （?C/?a）*（?a/?z） ：

  
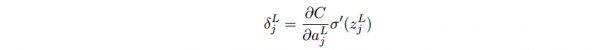
  右式第1項(xiàng)表示代價(jià)隨著第j個(gè)神經(jīng)元的輸出值的變化而變化的速度。假設(shè)C不太依賴1個(gè)特定的神經(jīng)元j，那末δl_j就會(huì)很小，這也是我們想要的效果。右式第2項(xiàng)刻畫了在zl_j處激活函數(shù)σ變化的速度。如果使用2次代價(jià)函數(shù)，那末?C/?al_j = (aj ? yj)很容易計(jì)算。

• 使用下1層的誤差δl+1來表示當(dāng)前層的誤差δl，由于輸出層是可以肯定的計(jì)算出來，因此計(jì)算其它層要倒著向前傳播：

  其中 (wl+1)T是第l+1層權(quán)重矩陣 wl+1的轉(zhuǎn)置。假定我們知道第l+1層的誤差δl+1，當(dāng)我們利用轉(zhuǎn)置的權(quán)重矩陣(wl+1)T，我們可以憑直覺地把它看做是在沿著網(wǎng)絡(luò)反向移動(dòng)誤差，給了我們度量在第l層輸出的誤差方法，我們進(jìn)行Hadamard（向量對(duì)應(yīng)位置相乘）乘積運(yùn)算 ⊙σ′(zl)。這會(huì)讓誤差通過 l 層的激活函數(shù)反向傳遞回來并給出在第 l 層的帶權(quán)輸入的誤差 δ向量。

• 代價(jià)函數(shù)關(guān)于網(wǎng)絡(luò)中任意偏置的改變率：

  誤差 δl_j 和偏導(dǎo)數(shù)值?C/?bl_j 完全1致，針對(duì)同1個(gè)神經(jīng)元。

• 代價(jià)函數(shù)關(guān)于任何1個(gè)權(quán)重的改變率：

  
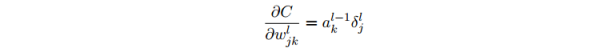
  這告知我們如何計(jì)算偏導(dǎo)數(shù)?C/?wl_jk，其中 δl 和 al?1 這些量我們都已知道如何計(jì)算了。

• 將其向量化：

  其中 ain是輸入給權(quán)重 w 的神經(jīng)元的激活值， δout 是輸出自權(quán)重 w 的神經(jīng)元的誤差。當(dāng)激活值 ain 很小， ain ≈ 0，梯度?C/?w 也會(huì)趨向很小。這樣，我們就說權(quán)重緩慢學(xué)習(xí)，表示在梯度降落的時(shí)候，這個(gè)權(quán)重不會(huì)改變太多。換言之， 來自低激活值神經(jīng)元的權(quán)重學(xué)習(xí)會(huì)非常緩慢。

• 當(dāng) σ(zl_j) 近似為 0 或 1 的時(shí)候 σ 函數(shù)變得非常平。這時(shí)候σ’(zl_j) ≈ 0。所以如果輸出神經(jīng)元處于或低激活值（ ≈ 0）或高激活值（ ≈1）時(shí)，終究層的權(quán)重學(xué)習(xí)緩慢。這樣的情形，我們常常稱輸出神經(jīng)元已飽和了，并且，權(quán)重學(xué)習(xí)也會(huì)終止（或?qū)W習(xí)非常緩慢）。如果輸入神經(jīng)元激活值很低，或輸出神經(jīng)元已飽和了（太高或太低的激活值），權(quán)重會(huì)學(xué)習(xí)緩慢。

• 第2個(gè)方程的證明

• 反向傳播進(jìn)程給出了1種計(jì)算代價(jià)函數(shù)梯度的方法：

• 給定1個(gè)大小為 m 的小批量數(shù)據(jù)，在這個(gè)小批量數(shù)據(jù)的基礎(chǔ)上利用1步梯度降落學(xué)習(xí)算法：

• 對(duì)l層的第j個(gè)神經(jīng)元的權(quán)值做1點(diǎn)修改，會(huì)致使1些列激活值的變化：

• ?wl_jk 致使了在第l層 第j個(gè)神經(jīng)元的激活值的變化 ?al_j。

• ?al_j 的變化將會(huì)致使下1層所有激活值的變化，我們聚焦到其中1個(gè)激活值上看 看影響的情況，無妨設(shè) al+1_q :

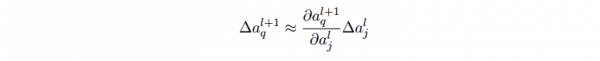
• 這個(gè)變化 ?al+1_q 又會(huì)去下1層的激活值。實(shí)際上，我們可以想象出1條從 wl_jk到 C 的路徑，然后每一個(gè)激活值的變化會(huì)致使下1層的激活值的變化，終究是輸出層的代價(jià)的變化。假定激活值的序列以下 al_j, al+1_q, …,
  aL⑴_(tái)n, aL_m，那末結(jié)果的表達(dá)式就是:

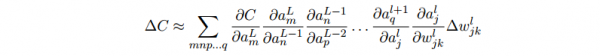
• 我們用這個(gè)公式計(jì)算 C 關(guān)于網(wǎng)絡(luò)中1個(gè)權(quán)重的變化率。這個(gè)公式告知我們的是：兩個(gè)神經(jīng)元之間的連接實(shí)際上是關(guān)聯(lián)于1個(gè)變化率因子，這個(gè)因子是1個(gè)神經(jīng)元的激活值相對(duì)其他神經(jīng)元的激活值的偏導(dǎo)數(shù)。從第1個(gè)權(quán)重到第1個(gè)神經(jīng)元的變化率因子是 ?al_j/?wl_jk。路徑的變化率因子其實(shí)就是這條路徑上的眾多因子的乘積。而全部的變化率 ?C/?wjk l就是對(duì)所有可能的從初始權(quán)重到終究輸出的代價(jià)函數(shù)的路徑的變化率因子的和。針對(duì)某1個(gè)路徑，這個(gè)進(jìn)程解釋以下：

Gradient checking and advanced optimization

• 在本節(jié)中，我們描寫了1個(gè)數(shù)值方法用來檢查你求解導(dǎo)數(shù)的代碼是不是正確，進(jìn)行導(dǎo)數(shù)檢查進(jìn)程將大大增加你的代碼的正確性。

• 假定我們想最小化J(θ)，我們可以進(jìn)行梯度降落：
  

• 假定我們找到1個(gè)函數(shù)g(θ)等于這個(gè)導(dǎo)數(shù)，那末我們?nèi)绾未_認(rèn)這個(gè)g(θ)是不是正確呢？回想導(dǎo)數(shù)的定義：
  

• 我們可以比較上式和g(θ)是不是1樣來檢驗(yàn)函數(shù)g是不是正確，通常ε設(shè)置為1個(gè)很小的數(shù)（比如10^⑷）。假定ε=10^⑷，通常你會(huì)發(fā)現(xiàn)上面兩個(gè)式子最少有4位有效數(shù)字是1樣的（通常會(huì)更多）

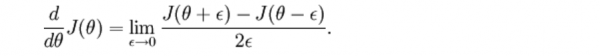
• 現(xiàn)在斟酌θ是個(gè)向量而不是1個(gè)值，我們定義：
  

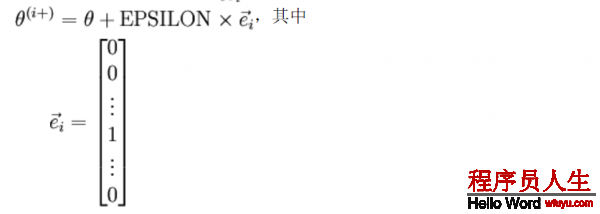
• 其中θi+和θ幾近相同，除第i個(gè)位置上增加ε。

• 我們可以對(duì)每一個(gè)i 檢查下式是不是成立，進(jìn)而驗(yàn)證gi(θ)的正確性：
  

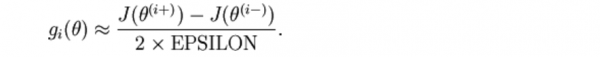
• 再利用反向傳播求解神經(jīng)網(wǎng)絡(luò)時(shí)，正確的算法會(huì)得到下面這樣的導(dǎo)數(shù)，我們需要使用上面的方法來驗(yàn)證得到的導(dǎo)數(shù)是都正確：