深度緩存（Z緩存）的研究

深度緩存（Z緩存）的研究

最近在shadow map進程中卡住了。由于我想在OpenGL ES 2.0兼容的平臺上運行shadow map，而要順利運行shadow map，通常的情況是具有GL_OES_depth_texture擴大，而有些兼容的機器是沒有這個擴大，這給我們開發人員帶來了1些難度。不過辦法還是有的，條件是要對計算機圖形學的Z-Buffer要有1個深入的了解才行。

蔣彩陽原創文章，首發地址：http://blog.csdn.net/gamesdev/article/details/44939923。歡迎同行前來探討。

參考維基百科上對Z-Buffer的介紹（這里第1個公式極可能是毛病的，感覺是2far?near而不是⑵far?near），當場景中的頂點在做MVP變換的時候，它的Z值也會遭到相應的變化。這里我們特別關注的是在視角空間下的頂點位置（X_e, Y_e, Z_e），在經過投影矩陣的變換時候會產生甚么變化。

首先是根據投影矩陣，對頂點進行投影變換：

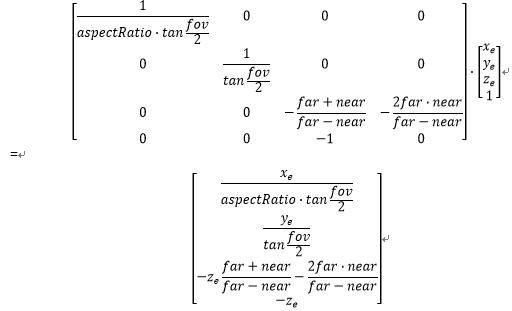
然后將齊次坐標轉換成為普通坐標，即同除以-Z_e進行規格化，讓第4個份量為1：

這個時候Z_ndc=了。

在NDC（Normalized Device Coordinates）坐標系轉化為屏幕坐標系的進程中，Z值也要被線性插值。此時的Z_ndc∈[⑴,1]的，首先需要插值到[0,1]中，然后根據深度的位數（1般是16、24和32位，幾近不存在8位的深度了），來平均映照過去。

這時候有：Z_w=S?[（Z_ndc/2）+0.5]

其中S=2ⁿ⑴，n是系統設定的深度位數。

即

以Z_e作為Z_w的函數，并化簡，則為：

我們可以大致地看到，Z_e和Z_w是成反比的（和1/Z_w成正比）。為了詳細了解相干情況，我們對它求導數：

令

則

計算后得到

我們可以很快看出，當

時，獲得最小值。這也就說明無窮多的相機空間的距離只影響幾近于0的Z緩存，換句話說，1個位的Z緩存變化就要反應無窮長的相機空間距離變化。

那末這個最小值點能否取到呢？由于計算機的Z緩存的深度變化是Z_w∈[0,2ⁿ⑴]，那末1定滿足

這里左側的不等式滿足的充分必要條件是near

這要求near和far異號，但是我們通常是不會設置near和far異號的。所以右側的不等式不滿足。因此

在Z_w∈[0,2ⁿ⑴]上是單調遞增的，而Z_e在Z_w∈[0,2ⁿ⑴]上是單調遞減的。所以這反應出，Z緩存中將更多的精度（2進制位數）給了距離攝像機（或zNear）較近的物體，而遠處（或zFar較近）的物體，留給的Z緩存精度很少。所以Z緩存與zNear于zFar的遠近精度關系其實不是線性的。這要求我們將更多的物體放在近平面處，遠處的物體，可使用LOD手法將其疏忽顯示，避免出現z-fighting。同時由于這樣的特性，shadow map在不同遠近出也會顯現分辨率不1致的情況。這就要求我們使用Cascade Shadow Map（CSM）這樣的技術來解決問題了。

參考文獻：

OpenGL FAQ：https://www.opengl.org/archives/resources/faq/technical/depthbuffer.htm

深入探索透視矩陣：http://blog.csdn.net/popy007/article/details/1797121

Z-Buffering on Wikipedia：http://en.wikipedia.org/wiki/Z-buffering#Mathematics

疑問：

OpenGL FAQ里面的

d(ze / we) / d zw = - f * (f-n) * (1/s) / n

= -f * (f/n⑴) / s

多是毛病的，應當加上1對括號。成為

= -f * (f/(n⑴)) / s

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈