您當前位置：首頁 > php開源 > 綜合技術 > Leetcode: Unique Paths

Leetcode: Unique Paths

來源：程序員人生發布時間：2015-04-13 08:22:42 閱讀次數：2724次

題目：

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

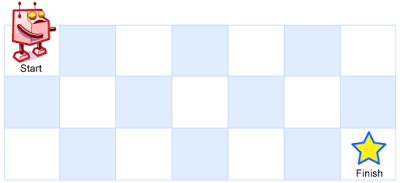
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

思路分析：

又是動態計劃問題。

開1個f[m][n]的數組，數組元素初始化為1，遞推公式f[i][j] = f[i⑴][j] + f[i][j⑴]，空間時間復雜度O(m*n)。

（可以將f[m][n]理解成為從f[0][0]到達f[m][n]的路徑個數。那很自然的就會f[i][j] = f[i⑴][j] + f[i][j⑴]。有感覺遞推公式還不是能很好想出來的，繼續加強訓練吧！）

C++參考代碼：

class Solution { public: int uniquePaths(int m, int n) { //將vector中的元素初始化為1 vector<vector<int>> v(m, vector<int>(n, 1)); for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { v[i][j] = v[i - 1][j] + v[i][j - 1]; } } return v[m - 1][n - 1]; } };

代碼還可以進1步優化。

由C(n,k) = C(n⑴,k) + C(n⑴,k⑴）；

對應于楊輝3角：

1 1

1 2 1

1 3 3 1

1 4 6 4 1

………………

所以利用楊輝3角，開1個f[n]的數組，數組元素初始化為1，遞推公式f[i]+=f[i⑴]，空間時間復雜度O(n)。

class Solution { public: int uniquePaths(int m, int n) { vector<int> v(n, 1); for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { v[j] += v[j - 1]; } } return v[n - 1]; } };

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈
程序員人生

------分隔線----------------------------

上一篇 項目部署到tomcat6.0啟動成功后訪問頁面報500錯誤解決方法

下一篇 并行和并發的區別進程和線程的區別

分享到:

------分隔線----------------------------

為碼而活

積分：4237

15粉絲

7關注

欄目熱點

多多色-多人伦交性欧美在线观看-多人伦精品一区二区三区视频-多色视频-免费黄色视屏网站-免费黄色在线

Leetcode: Unique Paths