[置頂] 動態規劃算法分析與探究

動態計劃算法分析與探究

摘 要：動態計劃是運籌學的1個分支。它是解決多階段決策進程最優化問題的1種方法。動態計劃就是為了使產生決策序列在符合某種條件下到達最優。動態計劃思想在各類信息學中頻繁的使用，其作用愈來愈遭到人們的重視。本文就動態計劃算法進行分析與探究，從而解決實際生活中的諸多問題。

引言

  算法是解決1系列問題的清晰指令，能夠在有限的時間內取得所要求的輸出。1個好的算法對解決1個或1類實際問題將給予很大幫助。評價1個算法優劣，主要體現在兩個方面（排除毛病算法的情況）。1、時間優劣性；2、空間優劣性。時間的優劣即在處理相同問題時，不同算法解決此問題所需的時間。時間的優劣換種方式表達就是算法的效力。另外一方面，是空間優劣即在處理相同問題時，不同算法解決此問題所需占用的資源（計算機資源），主要體現在所占用內存資源上。總的來講，算法優劣由時間復雜度和空間復雜度來衡量。

   對1種算法，判斷是不是是最優算法其實不能單單通過解決1個或1類問題來講明。由于，對1類的問題也許該算法的復雜度要低于其它算法，而解決另外一類問題的復雜度可能要高于其它算法。因此，沒有最好的算法，只有針對某1實際問題有最優的算法，該算法的時間復雜度和空間復雜度要低于其它算法。

1、動態計劃簡介

   1.1 動態計劃基本思想

   動態計劃的實質是分治思想和解決冗余，因此，動態計劃是1種將問題實例分解為更小的、相似的自問題，并存儲子問題的解而避免計算重復的自問題，已解決最優化問題的算法策略。

   動態計劃法所針對的問題有1個顯著的特點，即它所對應的子問題樹中的子問題顯現大量的重復。動態計劃法的關鍵就在于，對重復出現的子問題，只在第1次遇到時加以求解，并把答案保存起來，讓以后再遇到時直接援用，沒必要重新求解。

   1.2動態計劃分類

   動態計劃按其模型的不同可以分為：背包模型、最長非降子序列模型、最大字段和模型、LCS模型、線段覆蓋問題模型、股票模型、連續段劃分模型、游戲模型等。其中最為常見的就是背包問題，對背包問題可以再細分為：0⑴背包問題、無窮背包問題、有限背包問題、有價值背包、小數背包等問題。

2、動態計劃主要術語

  2.1 階段

   用動態計劃求解1個問題時，需要將問題的全進程恰當地劃分成若干個相互聯系的階段，以便按1定的次序去求解。階段的劃分1般是根據時間和空間的自然特點來定的，1般要便于把問題轉化成多階段決策的進程。

   2.2 狀態

   狀態表示的是事物某1階段的性質，狀態通過1個變量來描寫，這個變量稱為狀態變量。各個狀態之間是可以相互轉換的。

   2.3 決策

   對問題的處理中做出某種選擇性的行動就是決策。1個實際問題可能要有屢次決策，在每個階段中都需要有1次決策。1次決策就會從1個階段進入另外一個階段，狀態也就產生了轉移。

    2.4策略和最優策略

   所有階段依照約定的決策方法，順次排列構成問題的求解全進程。這些決策的整體稱為策略。在實際問題中，從決策允許集合中找出最優效果的策略稱為最優策略。

   2.5 狀態轉移方程

前1階段的終點就是后1階段的出發點，這類關系描寫了由K階段到K+1階段狀態的演化規律，是關于兩個相鄰階段狀態的方程，稱為狀態轉移方程，是動態計劃的核心。

3、應用動態計劃條件

   任何思想方法都有1定的局限性，超越了特定條件，它就失去了作用。同理，動態計劃也需滿足其使用條件。對解決動態計劃問題必須滿足最優化原理和無后效性。

  最優化原理：不管過去狀態和決策如何，對前面的決策所構成的狀態而言，余下的決策必須構成最優策略。簡而言之，1個最優化策略的自策略總是最優的。

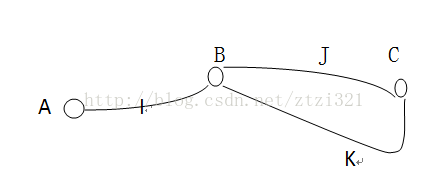
K

        (圖 1)

       如圖1所示，線路I和J是A到C的最優路徑，則根據最優化原理，線路J必須從B到C的最優線路。

   最優化原理是動態計劃的基礎，任何問題，如果失去了最優化原理的支持，就不可能用動態計劃方法計算。

       無后效性：“過去的步驟只能通過當前狀態影響未來的發展，當前的狀態是歷史的總結”。這條特點說明動態計劃只適用于解決當前決策與過去狀態無關的問題。狀態，出現在策略任何1個位置，它的地位相同，都可實行一樣策略，這就是無后效性。

4、動態計劃計算步驟

  4.1 劃分階段

   依照問題的時間或空間特點，將問題分為若干個階段。條件是這個若干個階段1定要有序，即無后向性。

   4.2 選擇狀態

   將問題發展到各個階段時所出現的各種客觀情況用不同的狀態表示。

   4.3 肯定決策并寫出狀態轉移方程

   狀態轉移就是根據上1階段的狀態和決策來導出本階段的狀態。

對動態計劃問題來講，階段的劃分是關鍵，必須根據題意分析，尋求公道的劃分階段的方法。根據計算最優值時得到的信息，構造問題的最優解。

接下來我用1個實例來講明解決動態計劃問題的步驟。

[問題描寫]：

設有1個正整數序列b₁，b₂，b₃，…，b_n，若下標為i₁<i₂<i₃<…<i_k且有b_i1≤b_i2≤… ≤b_ik則稱存在1個長度為k的不降落序列。可能有多個不降落序列，輸出最長序列的長度。

[樣例輸入]：

13　7　9　16　38　24　37　18

[樣例輸出]：

5               (7 9  16  24  37)

[問題分析]：

1、    分階段：以數的個數為階段。

2、    肯定狀態及狀態變量：n個數的最長不降落序列長度。

3、    決策：跟前面的哪一個數拼接成最長不降序列。

4、    策略和最優策略：終究解在那。

5、    狀態轉移方程：

[求解進程]：

1、以個數為階段，從第2項開始計算，由于前面唯一1項，所以做1次比較，因7<13，不符合問題要求，不作任何改變，長度仍為1。

2、第3項的前面有2項，因此需要做兩次比較，得到目前最長的不降落序列為2，情況以下表：

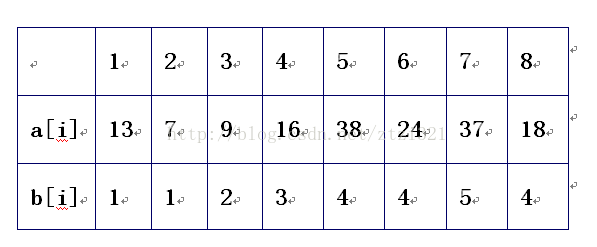
(圖 2)

3、處理進程：在1，2，……，i⑴項中，找出比a[i]小于等于的最長長度L；若L>0，則b[i]=L+1。

5、動態計劃小結

動態計劃所處理的問題是1個“多階段決策問題”，目的是得到1個最優解（方案）。動態計劃的實質是分治思想和解決冗余，因此，動態計劃是1種將問題分解為更小的、相似的子問題，并存儲子問題的解而避免計算重復的子問題，以解決最優化問題的算法策略。這類問題會有多種可能的解，每一個解都有1個值，而動態計劃找出其中最優（最大或最小）解。若存在多個最優解的話，它只取其中的1個。

(圖 3)

動態計劃與貪心算法類似，是通過量階段決策進程來解決問題的，同時動態計劃又與遞歸法類似，當問題不能分解為獨立的階段，卻又符合最優原理（最優子結構性質）時，就比較合適用動態計劃。

但動態計劃與1般的遞推不同點也比較明顯，主要表現以下方面：

1、遞推的邊界條件1般很明顯，而動態計劃的邊界條件比較隱蔽，容易被忽視；

2、遞推的數學性1般較強，而動態計劃的數學性相對較弱；

3、遞推1般不劃分階段，而動態計劃1般有較為明顯的階段；

4、動態計劃常常是用來求1個最優值，而1般的遞推常常是用來計數或是求1個值。

因此，總的來講，動態計劃更加合適解決絕大多數最優化問題。但是，動態計劃來解決問題其實不1定是最優（復雜度較低），因此，具體問題需要具體分析，從而肯定最優算法。

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈