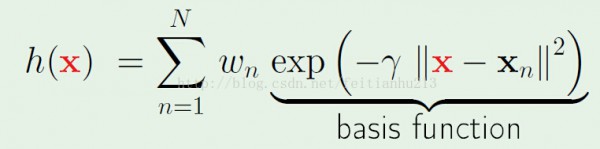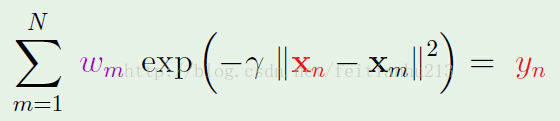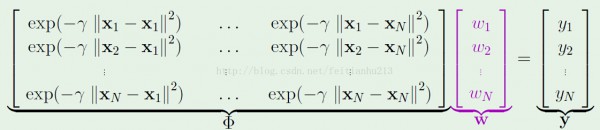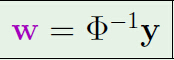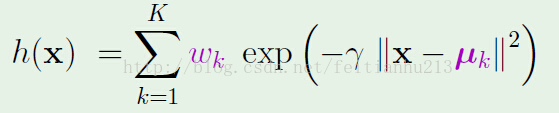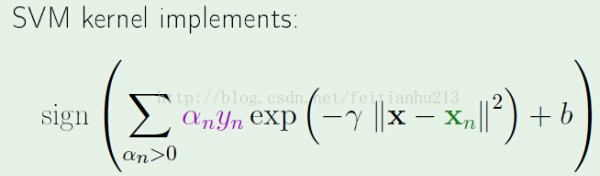[置頂] 加州理工學院公開課:機器學習與數據挖掘_Radial Basis Function(第十六課)
來源:程序員人生 發布時間:2015-02-02 08:32:25 閱讀次數:3974次
課程簡介 :
主要介紹了 RBF 模型及其與最近鄰算法、神經網絡、Kernel Method 的比較。最后介紹了 RBF 模型的 regularization 問題。
課程提綱 :
1、what is RBF
2、RBF and nearest neighbors
3、RBF and neural networks
4、RBF and kernel methods
5、RBF and regularization
1、what is RBF
RBF 是基于半徑的1個模型。由于訓練集中的每個點都會對訓練集(h(x))造成影響,但是影響的方式會因問題而異。這1節課主要討論的是訓練集中的點對模型的影響是基于:||X-Xn|| 的情勢的。也就是說是基于半徑的(based on radial )。
標準情勢:(下面的模型是高斯散布模型,固然也能夠用其它的模型,但是既然是radial based,那末就必須得存在||x-xn||項)
有了模型,我們還需要學習它的參數,上述公式中的參數主要有兩個:wn 和 γ。γ 會影響高斯散布曲線的形狀(肥瘦)。現在暫時放下 γ 參數,先來看看如何學習 wn。
學習的條件是要有1個指點方針。這里的指點方針就是h(xm) == ym。 其中 ym 是數據的真實值(對分類問題就是標簽)。
所以我們的問題就是解下面的方程:(為了1致性,下述公式中的xm對應上述公式的 xn,下述公式中的 xn 對應上述公式中的 x)
用矩陣表示以下:
如果矩陣可逆,則有:(聽說可以利用插入法求解)
到目前為止,我們可以成功的利用訓練數據求得參數 W ,1切都很順利,那末是否是說明只要我們再把 γ 求出來就能夠了呢?
答案是不是定的,由于這里存在1個過擬化的問題。明顯上述的方法得到的解,對樣本內數據來講,誤差為 0,之前說過,這其實不是1件好事,由于這樣會致使泛化能力減弱。這里利用到的解決方法是:聚類。
2、RBF and nearest neighbors
對第1點中提到的過擬化問題,可以利用聚類方法進行解決。
基本思路:利用某種方法(比如:k-means)把訓練數據聚成 k 個類。每一個聚類中心代表該類進行訓練。
因此模型變成:
針對上述模型,存在兩個問題:
1、如何選擇 k 個中心點。
2、如何學習 wk。
第1點可以利用 k-means 方法解決。現在主要看看第2點:
由于現在參數 wk 變成k個,因此該模型會存在誤差,有:
通過解上述方程,我們可以求出 W(具體怎樣解?還得惡補線性代數。。。)
現在剩下的問題就是如何求解 γ 了。下面用到的方法叫做:混合高斯模型的期望最大化(EM algorithm in mixture of Gaussians)
第1步:固定 γ,求解 W
第2步:固定W,求出使模型誤差最小時對應的 γ。
第3步:跳回第1步,直到滿足終止條件。(迭代m次等。)
3、RBF and neural networks
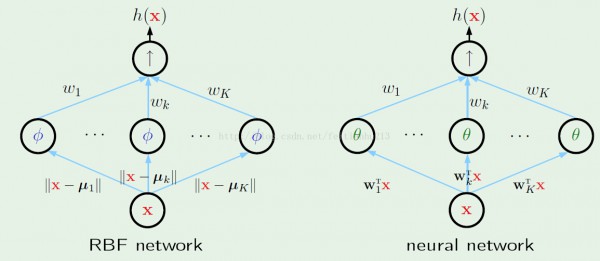
通過上面步驟,已可以求解出 RBF 模型了。現在看看其與神經網絡的比較:
通過上圖我們可以知道:
1、RBF network 和 neural network 在情勢上是1致的。
2、對 RBF network 第1級輸入參數是固定的:||x-μi||,但是對 neural network,對應的參數需要通過反向傳播進行學習。
3、對 RBF network 當第1級輸入值很大的時候,對應節點的輸出會變得很小(高斯模型),而對 neural network 則不存在這1特點,根具體節點使用的函數有關。
4、RBF and kernel methods
再來看看 RBF 與 SVM kernel 的對照。
首先在情勢上:
SVM kernel: RBF:
對 RBF ,增加額外的參數b,并且轉變成而分類問題。這樣是為了更方便地與 SVM kernel 比較。
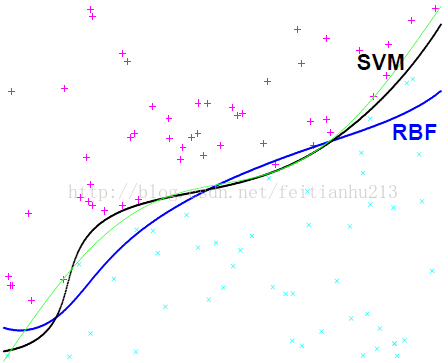
我們關心的第1個問題是:它們的表現如何? 下面的圖顯示了這兩個模型的表現(綠色線表示目標函數 ):
可以看到,雖然是來自兩個不同世界的模型,但是他們的表現卻很接近(SVM 更好1點),不過在具體的問題中,很難說清楚誰的效果更好。
注意,上圖中RBF 用到的聚類數量 k == svm 中的支持向量數。
5、RBF and regularization
注意:關于聚類中的 k 如何選擇?我開始認為是不是可以計算出 VC 維作為參考?在課堂最后的時候學生也問到這個問題,不過教授說不能這樣做。是 k -> VC 而不是 VC->k.
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈