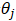梯度下降法及其Python實現
來源:程序員人生 發布時間:2016-06-17 08:45:28 閱讀次數:6156次
梯度降落法(gradient descent),又名最速降落法(steepest descent)是求解無束縛最優化問題最經常使用的方法,它是1種迭代方法,每步主要的操作是求解目標函數的梯度向量,將當前位置的負梯度方向作為搜索方向(由于在該方向上目標函數降落最快,這也是最速降落法名稱的由來)。
梯度降落法特點:越接近目標值,步長越小,降落速度越慢。
直觀上來看以下圖所示:
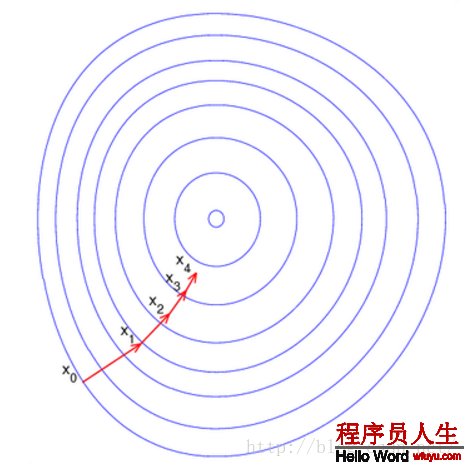
這里每個圈代表1個函數梯度,最中心表示函數極值點,每次迭代根據當前位置求得的梯度(用于肯定搜索方向和與步長共同決定前進速度)和步長找到1個新的位置,這樣不斷迭代終究到達目標函數局部最優點(如果目標函數是凸函數,則到達全局最優點)。
下面我們將通過公式來具體說明梯度降落法
下面這個h(θ)是我們的擬合函數
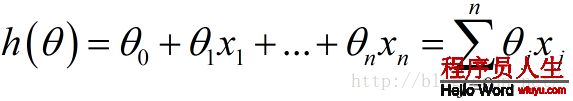
也能夠用向量的情勢進行表示:
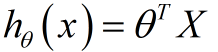
下面函數是我們需要進行最優化的風險函數,其中的每項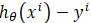 都表示在已有的訓練集上我們的擬合函數與y之間的殘差,計算其平方損失函數作為我們構建的風險函數(參見最小2乘法及其Python實現)
都表示在已有的訓練集上我們的擬合函數與y之間的殘差,計算其平方損失函數作為我們構建的風險函數(參見最小2乘法及其Python實現)
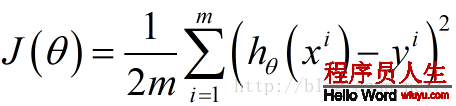
這里我們乘上1/2是為了方便后面求偏導數時結果更加簡潔,之所以能乘上1/2是由于乘上這個系數后對求解風險函數最優值沒有影響。
我們的目標就是要最小化風險函數,使得我們的擬合函數能夠最大程度的對目標函數y進行擬合,即:
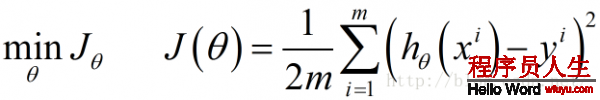
后面的具體梯度求解都是圍繞這個目標來進行。
批量梯度降落BGD
依照傳統的思想,我們需要對上述風險函數中的每一個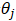 求其偏導數,得到每一個
求其偏導數,得到每一個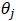 對應的梯度
對應的梯度
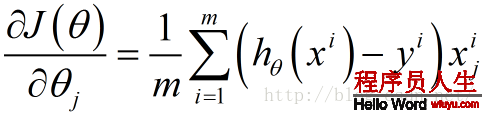
這里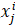 表示第i個樣本點
表示第i個樣本點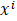 的第j份量,即h(θ)中的
的第j份量,即h(θ)中的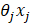
接下來由于我們要最小化風險函數,故依照每一個參數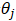 的負梯度方向來更新每個
的負梯度方向來更新每個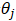
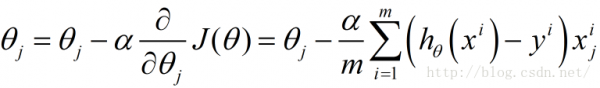
這里的α表示每步的步長
從上面公式可以注意到,它得到的是1個全局最優解,但是每迭代1步,都要用到訓練集所有的數據,如果m很大,那末可想而知這類方法的迭代速度!!所以,這就引入了另外1種方法,隨機梯度降落。
隨機梯度降落SGD
由于批量梯度降落在訓練集很大的情況下迭代速度非常之慢,所以在這類情況下再使用批量梯度降落來求解風險函數的最優化問題是不具有可行性的,在此情況下,提出了——隨機梯度降落
我們將上述的風險函數改寫成以下情勢:
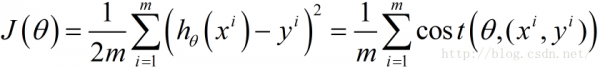
其中,
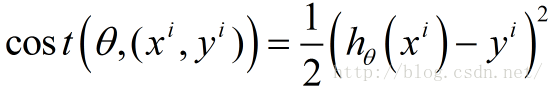
稱為樣本點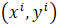 的損失函數
的損失函數
接下來我們對每一個樣本的損失函數,對每一個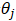 求其偏導數,得到每一個
求其偏導數,得到每一個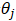 對應的梯度
對應的梯度
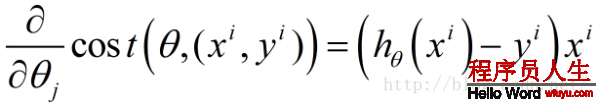
然后根據每一個參數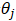 的負梯度方向來更新每個
的負梯度方向來更新每個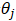
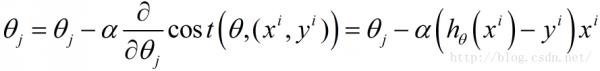
與批量梯度降落相比,隨機梯度降落每次迭代只用到了1個樣本,在樣本量很大的情況下,常見的情況是只用到了其中1部份樣本數據便可將θ迭代到最優解。因此隨機梯度降落比批量梯度降落在計算量上會大大減少。
SGD有1個缺點是,其噪音較BGD要多,使得SGD其實不是每次迭代都向著整體最優化方向。而且SGD由于每次都是使用1個樣本進行迭代,因此終究求得的最優解常常不是全局最優解,而只是局部最優解。但是大的整體的方向是向全局最優解的,終究的結果常常是在全局最優解附近。
下面是兩種方法的圖形展現:
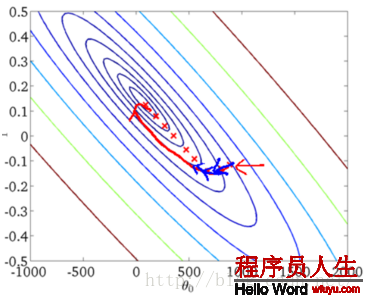
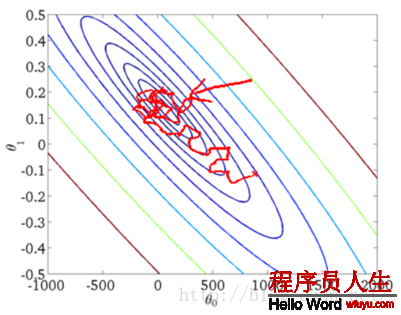
從上述圖形可以看出,SGD由于每次都是用1個樣本點進行梯度搜索,因此其最優化路徑看上去比較盲目(這也是隨機梯度降落名字的由來)。
對照其優劣點以下:
批量梯度降落:
優點:全局最優解;易于并行實現;整體迭代次數不多
缺點:當樣本數目很多時,訓練進程會很慢,每次迭代需要耗費大量的時間。
隨機梯度降落:
優點:訓練速度快,每次迭代計算量不大
缺點:準確度降落,其實不是全局最優;不容易于并行實現;整體迭代次數比較多。
============ 分割分割 =============
上面我們講授了甚么是梯度降落法,和如何求解梯度降落,下面我們將通過Python來實現梯度降落法。
# _*_ coding: utf⑻ _*_
# 作者: yhao
# 博客: http://blog.csdn.net/yhao2014
# 郵箱: yanhao07@sina.com
# 訓練集
# 每一個樣本點有3個份量 (x0,x1,x2)
x = [(1, 0., 3), (1, 1., 3), (1, 2., 3), (1, 3., 2), (1, 4., 4)]
# y[i] 樣本點對應的輸出
y = [95.364, 97.217205, 75.195834, 60.105519, 49.342380]
# 迭代閥值,當兩次迭代損失函數之差小于該閥值時停止迭代
epsilon = 0.0001
# 學習率
alpha = 0.01
diff = [0, 0]
max_itor = 1000
error1 = 0
error0 = 0
cnt = 0
m = len(x)
# 初始化參數
theta0 = 0
theta1 = 0
theta2 = 0
while True:
cnt += 1
# 參數迭代計算
for i in range(m):
# 擬合函數為 y = theta0 * x[0] + theta1 * x[1] +theta2 * x[2]
# 計算殘差
diff[0] = (theta0 + theta1 * x[i][1] + theta2 * x[i][2]) - y[i]
# 梯度 = diff[0] * x[i][j]
theta0 -= alpha * diff[0] * x[i][0]
theta1 -= alpha * diff[0] * x[i][1]
theta2 -= alpha * diff[0] * x[i][2]
# 計算損失函數
error1 = 0
for lp in range(len(x)):
error1 += (y[i]-(theta0 + theta1 * x[i][1] + theta2 * x[i][2]))**2/2
if abs(error1-error0) < epsilon:
break
else:
error0 = error1
print ' theta0 : %f, theta1 : %f, theta2 : %f, error1 : %f' % (theta0, theta1, theta2, error1)
print 'Done: theta0 : %f, theta1 : %f, theta2 : %f' % (theta0, theta1, theta2)
print '迭代次數: %d' % cnt
結果(截取部份):
theta0 : 2.782632, theta1 : 3.207850, theta2 : 7.998823, error1 : 7.508687
theta0 : 4.254302, theta1 : 3.809652, theta2 : 11.972218, error1 : 813.550287
theta0 : 5.154766, theta1 : 3.351648, theta2 : 14.188535, error1 : 1686.507256
theta0 : 5.800348, theta1 : 2.489862, theta2 : 15.617995, error1 : 2086.492788
theta0 : 6.326710, theta1 : 1.500854, theta2 : 16.676947, error1 : 2204.562407
theta0 : 6.792409, theta1 : 0.499552, theta2 : 17.545335, error1 : 2194.779569
theta0 : 74.892395, theta1 : ⑴3.494257, theta2 : 8.587471, error1 : 87.700881
theta0 : 74.942294, theta1 : ⑴3.493667, theta2 : 8.571632, error1 : 87.372640
theta0 : 74.992087, theta1 : ⑴3.493079, theta2 : 8.555828, error1 : 87.045719
theta0 : 75.041771, theta1 : ⑴3.492491, theta2 : 8.540057, error1 : 86.720115
theta0 : 75.091349, theta1 : ⑴3.491905, theta2 : 8.524321, error1 : 86.395820
theta0 : 75.140820, theta1 : ⑴3.491320, theta2 : 8.508618, error1 : 86.072830
theta0 : 75.190184, theta1 : ⑴3.490736, theta2 : 8.492950, error1 : 85.751139
theta0 : 75.239442, theta1 : ⑴3.490154, theta2 : 8.477315, error1 : 85.430741
theta0 : 97.986390, theta1 : ⑴3.221172, theta2 : 1.257259, error1 : 1.553781
theta0 : 97.986505, theta1 : ⑴3.221170, theta2 : 1.257223, error1 : 1.553680
theta0 : 97.986620, theta1 : ⑴3.221169, theta2 : 1.257186, error1 : 1.553579
theta0 : 97.986735, theta1 : ⑴3.221167, theta2 : 1.257150, error1 : 1.553479
theta0 : 97.986849, theta1 : ⑴3.221166, theta2 : 1.257113, error1 : 1.553379
theta0 : 97.986963, theta1 : ⑴3.221165, theta2 : 1.257077, error1 : 1.553278
Done: theta0 : 97.987078, theta1 : ⑴3.221163, theta2 : 1.257041
迭代次數: 3443
可以看到最后收斂到穩定的參數值。
注意:這里在選取alpha和epsilon時需要謹慎選擇,可能不適的值會致使最后沒法收斂。
參考文檔:
隨機梯度降落(Stochastic gradient descent)和 批量梯度降落(Batch gradient descent
)的公式對照、實現對照
隨機梯度降落法
python實現梯度降落算法
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈


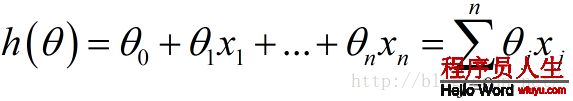
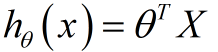
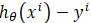 都表示在已有的訓練集上我們的擬合函數與y之間的殘差,計算其平方損失函數作為我們構建的風險函數(參見最小2乘法及其Python實現)
都表示在已有的訓練集上我們的擬合函數與y之間的殘差,計算其平方損失函數作為我們構建的風險函數(參見最小2乘法及其Python實現)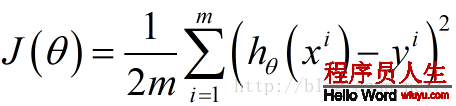
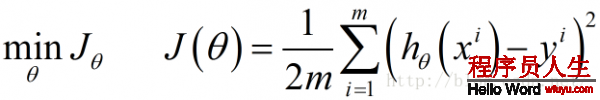
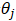 求其偏導數,得到每一個
求其偏導數,得到每一個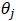 對應的梯度
對應的梯度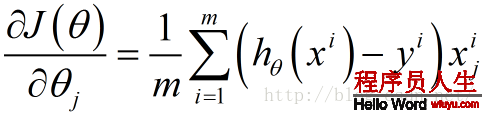
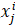 表示第i個樣本點
表示第i個樣本點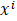 的第j份量,即h(θ)中的
的第j份量,即h(θ)中的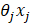
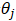 的負梯度方向來更新每個
的負梯度方向來更新每個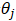
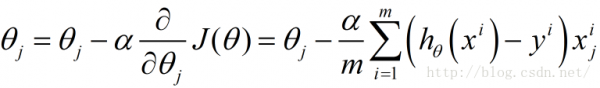
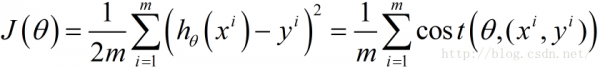
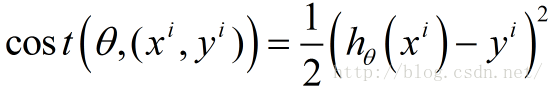
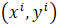 的損失函數
的損失函數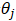 求其偏導數,得到每一個
求其偏導數,得到每一個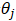 對應的梯度
對應的梯度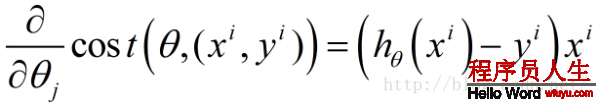
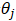 的負梯度方向來更新每個
的負梯度方向來更新每個