灰度圖像--頻域濾波 概論
來源:程序員人生 發(fā)布時間:2015-02-09 09:02:41 閱讀次數(shù):5493次
學習DIP第25天
轉載請標明本文出處:http://blog.csdn.net/tonyshengtan,歡迎大家轉載,發(fā)現(xiàn)博客被某些論壇轉載后,圖象沒法正常顯示,沒法正常表達本人觀點,對此表示很不滿意。有些網(wǎng)站轉載了我的博文,很開心的是自己寫的東西被更多人看到了,但不開心的是這段話被去掉了,也沒標明轉載來源,雖然這并沒有版權保護,但感覺還是不太好,出于尊重文章作者的勞動,轉載請標明出處!!!!
開篇空話
這兩天寫了1下頻域濾波的代碼,并且發(fā)現(xiàn)之前博客里代碼的1個BUG,產(chǎn)生BUG的緣由是1維存儲的2維矩陣行寬和列長被寫反了,而且測試沒有測出來,看來測試是必要的,而且還學習了下使用github,托管代碼,由于是小菜,托管HelloWorld也不丟人,頻域濾波打算寫兩到3篇,然后結束,進行下1大塊問題的研究。
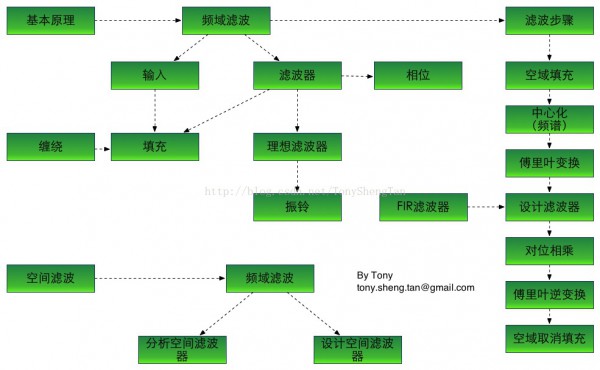
頻域濾波的主要知識框架作了1個結構圖,完全個人理解,如有理論上的問題,請及時指出:
頻域濾波基礎
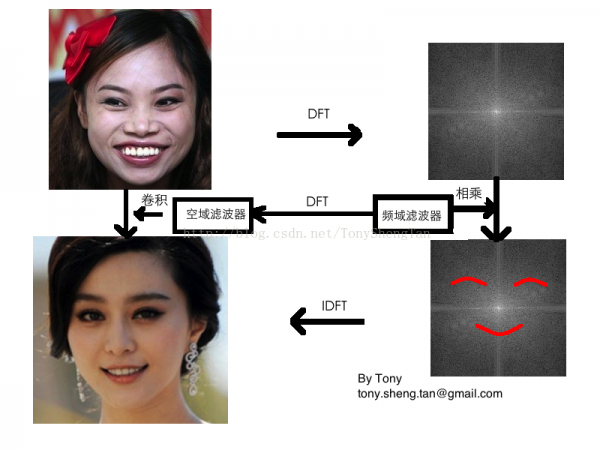
對空域濾波和時域濾波,其最重要的理論基礎就是,頻率域的高頻部份對應于空域中變化峻峭的細節(jié),而頻域的低頻部份對應于空域變化換面的平坦區(qū)域,為了得到平滑或峻峭的部份,我們就想到了頻域濾波,在空域中對細節(jié)和非細節(jié)的提取和定義并沒有頻域那末直接與明確,通過頻域這個實驗室,可以得出很多針對不同問題,特殊的濾波器,然后將其轉換到空域,生成小模板,使用卷積運算來完成快速的濾波,到達我們的目的。基本關系示意圖:
沒錯,冰冰和鳳姐就差1個濾波器!(此為示意圖,沒有這樣的濾波器,請勿模仿0.0)
我們的基本原理就是高頻對應變化峻峭的部份,低頻對應變化緩慢的部份。低頻和高頻在頻率域以數(shù)字度量,濾波器對頻域的數(shù)字進行不同程度的增強或抑制,以后進行逆變換,得到想要的圖象,頻域濾波器必須在頻域關于原點對稱,不然對稱部份頻率的逆變換將是原圖產(chǎn)生偽影效果。
影響頻域濾波效果的只有輸入和濾波器,對未處理的輸入,如果直接進行DFT和濾波的話,會產(chǎn)生糾纏效果,我們來看數(shù)學效果:
卷積定理表明:對3x3的兩個矩陣a和b的卷積,應當?shù)扔赼的DFT和b的DFT對位相乘(對位相乘的意思就是對a和b對位相乘的結果c,c(x,y)=a(x,y)*b(x,y),而非1般的矩陣相乘),再進行IDFT變換,就能夠得到和空域的卷積結果,但我們得到的結果是:
clear all;clc;
a=[1 2 1;1 1 1 ;0 2 1];
fa=fft2(a);
b=[3 2 1;3 1 1 ;2 0 1];
fb=fft2(b);
temp=eye(3);
for R=1:3
for C=1:3
temp(R,C)=fa(R,C)*fb(R,C);
end
end
res=ifft2(temp);
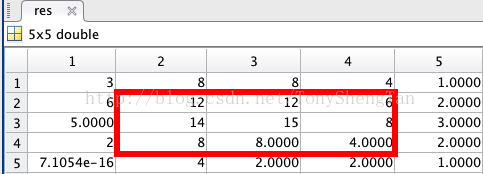
通過我們用手計算,發(fā)現(xiàn)結果不對,這是甚么緣由呢,我們暫時不說緣由,我們把矩陣用0擴充到5x5:
clear all;clc;
a=[1 2 1 0 0;1 1 1 0 0;0 2 1 0 0;0 0 0 0 0;0 0 0 0 0];
fa=fft2(a);
b=[3 2 1 0 0;3 1 1 0 0;2 0 1 0 0;0 0 0 0 0;0 0 0 0 0];
fb=fft2(b);
temp=eye(5);
for R=1:5
for C=1:5
temp(R,C)=fa(R,C)*fb(R,C);
end
end
res=ifft2(temp);
沒錯,看紅色框框,和我們用筆算的3x3的結果1樣;
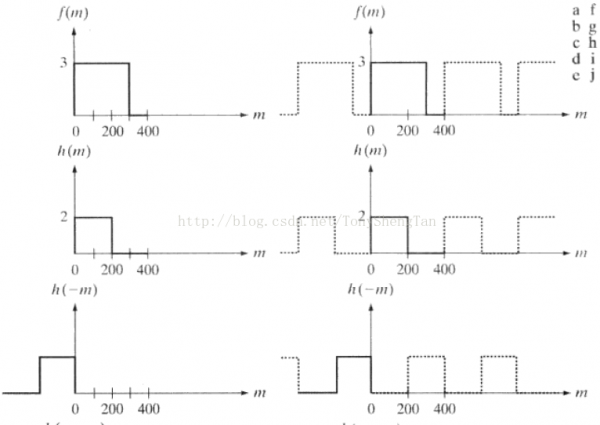
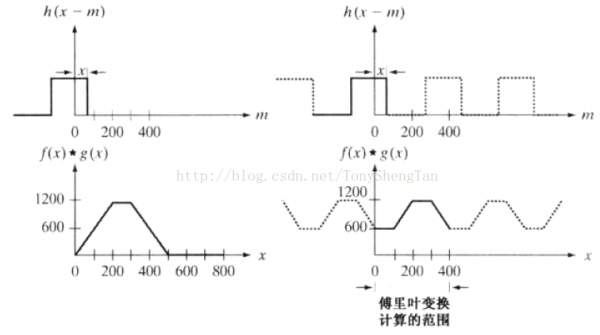
緣由是,如果對1個有限寬度為A的信號使用寬度為B的窗進行卷積,那末結果將會是1個寬度為A+B⑴的信號,但如果信號寬度為A但周期也是A即信號尾部和下1個周期的頭是緊挨著的話,那末進行卷積的時候尾部的信號就會和頭部的信號相互糾纏,使結果的頭部和尾部遭到污染,中間部份保持正確,但如果信號比較短,就像上面3x3的話就完全被污染了。
但上面的信號是其實不是周期的,而是有限寬度的,問題就出在DFT上,由于DFT把信號擴充了,而且是周期性的擴充,DFT時信號實際上是這樣的:
所以DFT的兩個信號就是周期的而不是我們之前輸入的信號,所以就會產(chǎn)生糾纏
避免這個問題很簡單,對兩個矩陣都用用0進行填充,填充成5x5后,得到正確的卷積結果。
濾波器的特性,濾波器是對傅里葉譜的實部和虛部進行等比增強或抑制,也就是傅里葉譜經(jīng)過濾波器后,相位是沒有變化的,主要緣由之條件到過,就是1個譜的相角決定了圖片的主要結構特點,所以,如果改變相角,那圖片將產(chǎn)生巨大問題,所以使用的濾波器都是0相移的,但如果使用非0相移可以得到其他目的的結果,比如讓1幅圖面目全非。
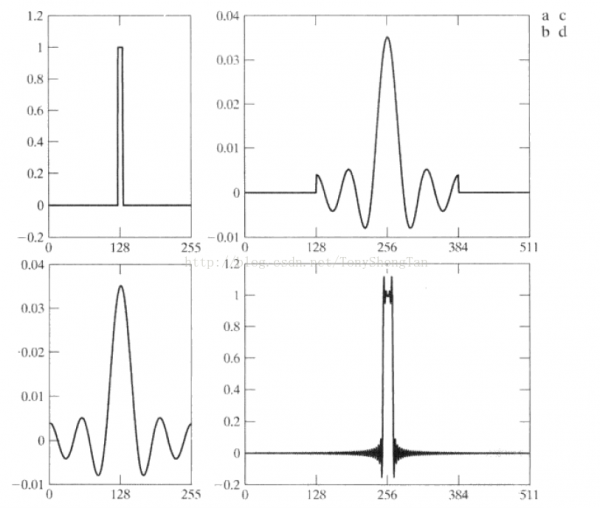
對理想濾波器,我們必須斟酌其擴充問題,緣由是,離線理想濾波器是頻域的,其擴充應當在空域進行,而理想濾波器的IDFT在空域不是有限的而是1個無窮的sinc函數(shù),進行階段后再填充,返回頻率域后填充后的濾波器將產(chǎn)生嚴重的振鈴現(xiàn)象,這里我們的辦法是只對圖象進行填充,填充到原圖的4倍大小,然后使用填充后大小的濾波器,來減輕纏繞問題,同時時使問題簡單化,但只是減緩纏繞問題,振鈴問題仍然存在。
上圖a為頻率域1維理想濾波器,b為IDFT后的空間波形,c是進行填充,d是填充后DFT的結果
下面我來解釋下振鈴現(xiàn)象,來個官方的解釋:
振鈴效應(Ringingeffect)是影響復原圖象質(zhì)量的眾多因素之1,其典型表現(xiàn)是在圖象灰度劇烈變化的鄰域出現(xiàn)類吉布斯(Gibbs)散布--(滿足給定束縛條件且熵最大的散布)的振蕩。在圖象盲復原中,振鈴效應是1個不可忽視的問題,其嚴重下降了復原圖象的質(zhì)量,并且使得難于對復原圖象進行后續(xù)處理。振鈴效應是由于在圖象復原當選取了不適當?shù)膱D象模型釀成的;在圖象盲復原中如果點分散函數(shù)選擇不準確也是引發(fā)復原結果產(chǎn)生振鈴效應的另外一個緣由,特別是選用的點分散函數(shù)尺寸大于真實點分散函數(shù)尺寸時,振鈴現(xiàn)象更加明顯;振鈴效應產(chǎn)生的直接緣由是圖象退化進程中信息量的丟失,特別是高頻信息的丟失。
官方解釋可能不好理解,在頻域理想濾波器情況下,其實就是sinc函數(shù)產(chǎn)生的,只斟酌上圖的a和b,a是頻域理想濾波器,b就是空域與之對應的濾波器,圖象如果和b卷積,結果必定產(chǎn)生類似波浪1樣的噪聲,圖象邊沿將會產(chǎn)生抖動,邊沿變寬,這就是振鈴效果,我們來視察不同截止頻率的理想濾波器和其IDFT效果:
可以看出越寬(截止頻率大)的濾波器頻域振鈴越步明顯,相反,越窄的濾波器,空域振鈴效果越大。
頻域濾波進程
頻率域濾波的進程:由于我們要得到的是圖象,輸入是圖象,輸出也是圖象,這個進程叫圖象處理,如果輸出的時頻譜或其他的,我們叫圖象分析,濾波器的主要參數(shù)是類型和截止頻率。
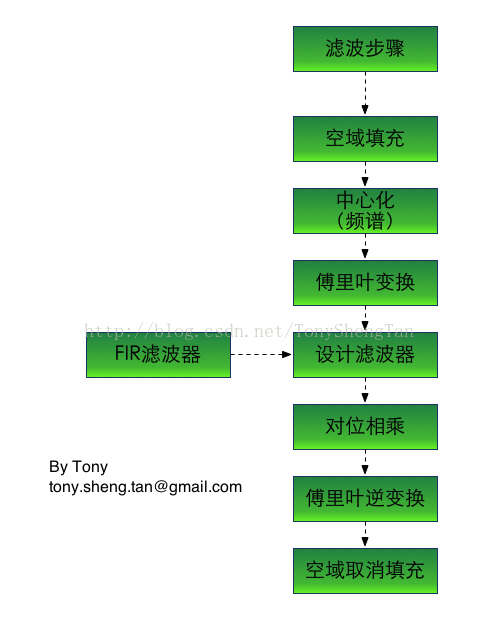
下面來看1下算法的完全計算進程:
原圖:
空域填充:
用0對圖片進行填充,得到4倍原圖的新圖象
頻譜中心化
這是為了配合濾波器,由于濾波器1般被設計為中間為低頻,4周為高頻的模式
DFT:
過度到頻域
設計濾波器
FIR濾波器,有限長單位沖激響應濾波器,又稱為非遞歸型濾波器,圖象處理中都使用這類濾波器產(chǎn)生1個高斯低通濾波器:
對位相乘:
IDFT:
將濾波結果重建為圖象
空域取消填充:
將填充過的圖象恢復
代碼:
#include "filter.h"
static void showfilter(double *filter,int width,int height){
IplImage *show=cvCreateImage(cvSize(width, height),8,1);
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
cvSetReal2D(show, j, i, filter[i*width+j]*255.0);
}
cvNamedWindow("Filter", 1);
cvShowImage("Filter", show);
cvWaitKey(0);
cvSaveImage("/Users/Tony/DIPImage/step.jpg", show, 0);
cvReleaseImage(&show);
}
void MatrixMulti_R_C(double *src1,Complex *src2,Complex *dst,int size){//m(1,1)=a(1,1)*b(1,1);
for(int i=0;i<size;i++){
dst[i].real=src2[i].real*src1[i];
dst[i].imagin=src2[i].imagin*src1[i];
}
}
int ChangtoPower2(int size){
size--;//避免為2的冪的size會被擴大
int i=0;
while ((size/=2)>0) {
i++;
}
return 2<<i;
}
//將圖象伸縮到2的冪次大小,并填充
void ResizeMatrix4FFT(IplImage *src,IplImage **dst){
int width=src->width;
int height=src->height;
int re_width=ChangtoPower2(width);
int re_height=ChangtoPower2(height);
IplImage *temp=cvCreateImage(cvSize(re_width, re_height), src->depth, src->nChannels);
cvResize(src, temp, 0);
*dst=cvCreateImage(cvSize(re_width*2, re_height*2), src->depth, src->nChannels);
cvZero(*dst);
for(int i=0;i<re_width;i++)
for(int j=0;j<re_height;j++)
cvSetReal2D(*dst, j, i, cvGetReal2D(temp, j, i));
cvReleaseImage(&temp);
}
//將擴充后的圖象還原為左上角的
void CutImage421(IplImage *src,IplImage *dst){
//IplImage *temp=cvCreateImage(cvSize(src->width/2, src->height/2), src->depth, src->nChannels);
int width=dst->width;
int height=dst->height;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++)
cvSetReal2D(dst, j, i, cvGetReal2D(src, j, i));
}
//頻域濾波
void FrequencyFiltering(IplImage *src,IplImage *dst,int filter_type,double param1,int param2){
IplImage *temp=NULL;
//調(diào)劑至2的冪,并用黑色填充,避免周期纏繞
ResizeMatrix4FFT(src, &temp);
int fft_width=temp->width;
int fft_height=temp->height;
//產(chǎn)生濾波器
double *filter=(double *)malloc(sizeof(double)*fft_height*fft_width);
if(filter==NULL){
printf("frequency filter malloc faile");
exit(0);
}
//生成濾波器
switch(filter_type){
case ILPF:
IdealLPFilter(filter, fft_width, fft_height, param1);
break;
case BLPF:
if(param2<0)
param2=2;
ButterworthLPfilter(filter, fft_width, fft_height, param1, param2);
break;
case GLPF:
GaussianLPFilter(filter, fft_width, fft_height, param1);
break;
case IHPF:
IdealHPFilter(filter, fft_width, fft_height, param1);
break;
case BHPF:
if(param2<0)
param2=2;
ButterworthHPfilter(filter, fft_width, fft_height, param1, param2);
break;
case GHPF:
GaussianHPFilter(filter, fft_width, fft_height, param1);
break;
}
//FFT
Complex *temp_complex=(Complex*)malloc(sizeof(Complex)*fft_height*fft_width);//fft結果
if(temp_complex==NULL){
exit(0);
}
ImageFFT(temp, temp_complex);
//相乘
MatrixMulti_R_C(filter,temp_complex,temp_complex,fft_width*fft_height);
//IFFT
ImageIFFT(temp_complex, temp, temp->width, temp->height);
//還原圖象
IplImage *result2=cvCreateImage(cvSize(temp->width/2, temp->height/2), temp->depth, temp->nChannels);
CutImage421(temp, result2);
cvResize(result2, dst, 0);
free(filter);
free(temp_complex);
cvReleaseImage(&temp);
cvReleaseImage(&result2);
}
空域濾波與頻域濾波
空域和頻域的橋梁是傅里葉變換,而紐帶是卷積定理,對頻域的特性,我們將其看作1個實驗室,進行實驗并產(chǎn)生小的濾波模板,將小的濾波模板對空域圖象進行循環(huán)卷積,得到我們想要的結果,空域小模板多半是奇數(shù)大小的(3x3,5x5)的,其計算復雜度低,進程簡單,用時較短,這就是之條件到的那個面試的問題的答案,如果我當時把這個進程給面試官講清楚,估計我現(xiàn)在就是1名圖象工作者了。
總結
這就是頻域濾波的基礎,后面的事情就是設計濾波器,滿足不同的問題,有了基礎,設計濾波器就要自己發(fā)揮了。
生活不易,碼農(nóng)辛苦
如果您覺得本網(wǎng)站對您的學習有所幫助,可以手機掃描二維碼進行捐贈

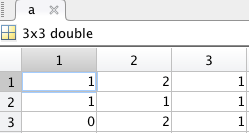 卷積
卷積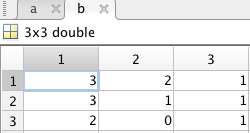 等于結果:
等于結果:
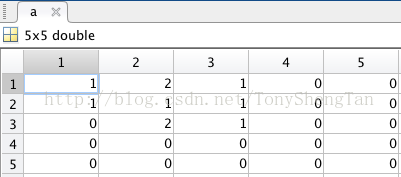 卷積
卷積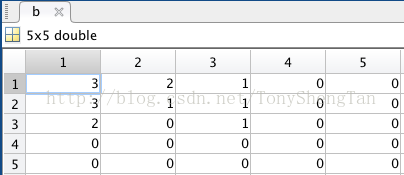 等于
等于