原文：http://en.wikipedia.org/wiki/No_free_lunch_in_search_and_optimization

說明：由于文章較難完全翻譯，所以部分句子采用了意譯的方法。此外，若發現翻譯錯誤之外，還望指證。

概述
      一些計算問題使用在候選解空間中進行搜索的方法來解決。搜索算法指如何選出候選解進行評價并重復這一過程的描述。對于特定問題，不同的搜索算法也許會得到不同的結果，但對于所有問題，它們是沒有性能差別的。也就是說如果一個算法在某些問題上得到較好的解，那么必然在另外的問題上得到較差的解。從這種意義上說，搜索領域沒有免費的午餐。此外，Schaffer說，搜索性能是守恒的。搜索通常可看作最優化，因此最優化問題也沒有免費的午餐。

     Wolpert和Macready的“沒有免費的午餐”理論淺顯地說起來就是任何兩個算法面對所有問題的平均性能都是等同的。沒有免費的午餐表明對不同問題選擇不同算法獲得的平均性能高于同一算法用在所有問題上。Igel，Toussaint以及English已經確定沒有免費午餐的一般情況。雖然這在理論上可能了，但實際情況卻不是100%與理論相吻合。Droste，Jansen，以及Wegener證明了一個定理——實際上“幾乎沒有免費的午餐”。

      將問題變得具體點，假設某個人要優化一個問題P。當他擁有問題是如何產生的知識，那么他可能利用這些知識找到一個專門處理P的算法。當然，這個算法有著很好的性能。當他不會利用這些知識或者他根本不知道這些知識，此時他的問題就變成找一個在大多數問題上都有較好性能的算法。“幾乎沒有免費的午餐”理論的作者說，他基本上不會找到，但將理論用到實際時，作者卻承認可能會有例外情況。

沒有免費的午餐（No free lunch，以下簡稱NFL）
      更正式地，“問題”是為目標函數找到好的候選解。搜索算法將目標函數作為輸入，然后一個個地評價候選解。最后輸出評價高的候選解序列。

      Wolpert和Macready約定一個算法決不會重新評價同一個候選解，算法的性能使用輸出來衡量。為簡單起見，我們不在算法中使用隨機函數。根據以上約定，搜索算法將每一個可能的輸入都運行一次，然后生成每一個可能的輸出一次。由于使用輸出衡量性能，不同算法取得特定水平的性能的頻繁程度是難以區分的。

     一些性能指標表明搜索算法在目標函數優化方面做得有多好。的確，將搜索算法用于優化問題，然后采用這種指標并不是什么另人驚奇的事。一種通常的指標是使用輸出序列中最差的解的最小下標，也就是最小化目標函數所需的評價次數。對于某些算法來說，找到最小值的時間與評價的次數成正比。

     原始的NFL理論假定全部的目標函數作為搜索算法的輸入都是等同的。不嚴格地說，已經確定當且僅當對目標函數進行“洗牌”后不影響輸出好結果的概率時，存在NFL（譯注：這句話不是很確定，求指教。原文是It has since been established that there is NFL if and only if, loosely speaking, "shuffling" objective functions has no impact on their probabilities）。盡管從理論來說，這種情況下是存在NFL的，但實際上必然不是精確的。

      顯然，不是NFL，就是“免費的午餐”了。但這是一種誤解。NFL是程度問題，不是有或者沒有的問題。如果會近似地出現NFL，那么所有算法對于一切目標函數所得到結果也是近似的。注意，“不是NFL”，僅僅意味著用某些性能指標衡量會出現算法不等同的情況。使用interest性能衡量時，各種算法也許仍然等同或近似等同（譯注：For a performance measure of interest中的interest，這里可能是專業術語，所以沒有翻譯）。

      理論上，全部算法處理優化問題時，通常能表現得不錯。也就說，算法對一切目標函數能使用相對較少的評價取得好的解。原因是幾乎全部的目標函數都有很大程度的Kolmogorov隨機性。這可以比作極度不規則和不可預測性。候選解等同地表示任一解，好的解全都分散在候選空間中。一個算法很少能只評價超過一小部分的候選解就得到一個非常好的解。

      事實上，幾乎全部的目標函數和算法都有如此之高的Kolmogorov復雜性以至于它們不出現上述情況。在典型的目標函數或者算法中的信息量比Seth Lloyd估計的可見領域能夠記錄的多。例如：如果一個候選解編碼為一個3000's和1's的序列（譯注：不理解encoded as a sequence of 300 0's and 1's中的單位），好的解是0和1，那么大多數的目標函數有著至少2^300位的kolmogorov復雜性。這大于Lloyd提出的10^90≈2^299的限界。由此可見，并非一切的物理現實都可以使用“沒有免費的午餐”理論。在實際意義上，一個“足夠小”的算法用在物理現實的應用中比那些不是的有著更好的性能。

NFL的正式簡介

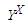     是所有目標函數f:X->Y的集合，其中X是一個有限的解空間，Y是有限的偏序集。令J為X的全排列的集合，F為分布在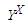上的一個隨機變量。對于J中的每一個j，F o j（譯注：注意中間那個o是集合論的右復合操作符）是分布在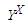上的隨機變量，其中對于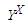中的全部都有P(F o j = f) = P(F = f o j^-1)

      令a(f)代表將輸入f用在搜索算法a上的輸出。假如a(F)和b(F)對于所有的算法a和b都有相同分布，那么就說F含有NFL分布。當且僅當F和F o j對于J中任意的j都是同分布的，這種情況才存在。換句話說，當且僅當目標函數在解空間的排列分布是不變的，就存在著沒有免費的午餐。

      當且僅當的條件是由C. Schumacher在他的博士論文Black Box Search - Framework and Methods中率先提出的。最近，集合論的NFL理論已經被廣義化為任意集X和Y

最初的NFL定理
      Wolpert和Macready給出兩個最重要的NFL定理。一個是關于在搜索過程中目標函數不會改變的。另一個是關于目標函數會改變的。
定理1：對于任一對算法a1和a2有

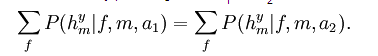
      大體上，這說明當所有函數f都是等可能出現時，在搜索過程中觀察到m值的任一個序列的概率并不依賴于所用的算法。定理2針對時變的目標函數建立了一個更精細的模型。

NFL結果解釋
      對NFL結果的一個易懂的但不是非常精確的解釋是“一個通用的通用型優化策略從理論上說是不存在的。一個策略表現得比其它策略好的唯一情況是將它用在專門處理的具體問題上。”以下是一些評論：

      一個幾乎通用的通用型算法理論上是存在的。每個搜索算法在幾乎所有的目標函數都能運行得很好。

      一個算法在不是專門處理的問題上可能也會表現得比另一個算法好。也許這個問題對于兩個算法來說都是最壞的問題。Wolpert和 Macready建立一個用來衡量一個算法與一個問題有多匹配的指標。就是說一個算法比另一個算法更好地匹配一個問題，而不是說其中的一個是專門處理這個問題。

      事實上，一些算法重新評價候選解。一個決不重新評價候選解的算法比另一個算法在一個特定的問題上更優秀，也許與這個問題是否為專門處理的問題無關。

      對于幾乎全部的目標函數，專門化從本質上來說是偶然的。不可壓縮性或者說 Kolmogorov 隨機性，使得目標函數在使用一個算法時沒有規律可尋。給出一個不可壓縮的目標函數，在不同算法之間的選擇并不存在偏好。如果一個選出來的算法比大多數的算法都要好，這個結果本身就是一個偶然事件。

     實際上，只有可高壓縮的（完全不是隨機的）目標函數才適合存儲于計算機中，不是每個算法都能在幾乎所有的可壓縮函數取得好的解。將問題的先驗知識加到算法中通常會帶來性能的提升。嚴格來說，當NFL出現時，對于處理優化問題的專業人員重要的是不要將“完全使用理論(full employment theorems)”按照字面意思來理解。首先，人們通常只有一點點的先驗知識。其次，將先驗知識加到算法處理某些問題時，帶來的性能提升甚微。最后，人類的時間比計算機的時間更寶貴。公司寧愿使用一個未經修改的程序來緩慢地優化一個函數，而不愿投入人力來開發一個更快的程序。這樣的例子屢見不鮮。

      NFL結果并不表明將算法用在一個不專門處理的問題上是無用的。沒有人能很快地判斷一個算法在實際問題的哪部分能取得好的解。此外，還存在著實際上的免費午餐，但這不與理論矛盾。在電腦上運行一個算法的實現比起使用人類時間和從好的解中得到利益的代價要小得多。假如這個算法成功地在可授受的時間內找到了令人滿意的解，那么這個小小的投資就取得了很大的回報。即使算法沒找到這樣的解，失去的也很少。

協同進化的免費午餐(Coevolutionary free lunches)
     Wolpert和Macready 已經證明在協同進化中存在免費的午餐。他們分析了covers'self-play'問題。在這些問題中，參與者們要通過在多人游戲中與一個或多個敵人對戰產生一個冠軍。也就是說，目的是不通過目標函數得到一個好的參與者。每個參與者（相當于候選解）的好壞通過在游戲中的表現得到的。一個算法嘗試通過參與者以及他們的游戲表現獲得好的參與者。算法將所有參與者中最好的一位當作冠軍。Wolpert和Macready已經證明一些協同進化算法得到冠軍質量通常比其它的算法要好。通過自我模擬(self-play)產生冠軍是進化計算以及博弈論有趣的地方。原因也很簡單，因為不能進化的物種自然就不是冠軍。