您當(dāng)前位置：首頁 > php開源 > php教程 > 數(shù)據(jù)結(jié)構(gòu)--排序算法總結(jié)

數(shù)據(jù)結(jié)構(gòu)--排序算法總結(jié)

來源：程序員人生發(fā)布時間：2017-02-04 09:03:40 閱讀次數(shù)：4375次

概述

排序的分類：內(nèi)部排序和外部排序

內(nèi)部排序：數(shù)據(jù)記錄在內(nèi)存中進(jìn)行排序

外部排序：因排序的數(shù)據(jù)量大，需要內(nèi)存和外存結(jié)合使用進(jìn)行排序

這里總結(jié)的8大排序是屬于內(nèi)部排序：

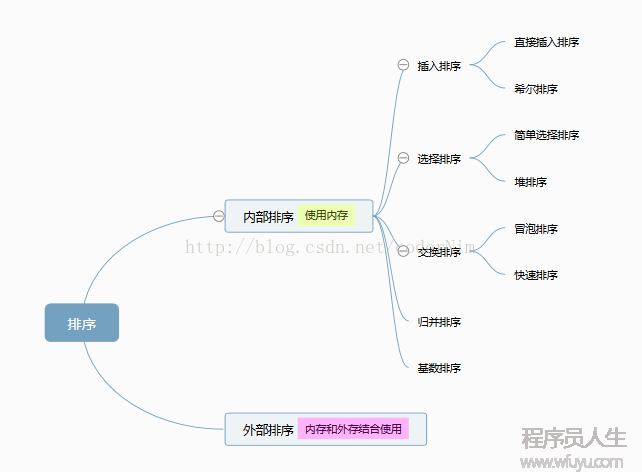
當(dāng)n比較大的時候，應(yīng)采取時間復(fù)雜度為（nlog2n）的排序算法：快速排序、堆排序或歸并排序。

其中，快速排序是目前基于比較的內(nèi)部排序中被認(rèn)為最好的方法，當(dāng)待排序的關(guān)鍵字是隨機(jī)散布時，快速排序的平均時間最短。

———————————————————————————————————————————————————————————————————————

插入排序——直接插入排序（Straight Insertion Sort）

基本思想：

將1個記錄插入到已排序好的有序表中，從而得到1個新的，記錄數(shù)增1的有序表。

即：先將序列的第1個記錄看成1個有序的子序列，然后從第2個記錄逐一進(jìn)行插入，直至全部序列有序為止。

要點：設(shè)立哨兵，用于臨時存儲和判斷數(shù)組邊界

直接插入排序示例：

插入排序是穩(wěn)定的，由于如果1個帶插入的元素和已插入元素相等，那末待插入元素將放在相等元素的后邊，所以，相等元素的前后順序沒有改變。

算法實現(xiàn)：

#include<iostream>
using namespace std;

void print(int a[], int n ,int i)
{  
    cout<<i<<":";  
    for(int j= 0; j<8; j++){  
        cout<<a[j] <<" ";  
    }  
    cout<<endl;  
} 

void InsertSort(int a[],int n)
{
	int i,j,tmp;
	for(i=1;i<n;++i)
	{
		// 如果第i個元素大于第i⑴個元素，直接插入
		// 否則
		// 小于的話，移動有序表后插入 
		if(a[i]<a[i⑴])
		{
			j=i⑴;
			tmp=a[i];	// 復(fù)制哨兵，即存儲待排序元素
			a[i]=a[i⑴];	// 前后移1個元素
			while(tmp<a[j])	 
			{	
				// 哨兵元素比插入點元素小，后移1個元素
				a[j+1]=a[j];
				--j;
			}
			a[j+1]=tmp;	// 插入到正確的位置 
		}
		print(a,n,i); // 打印每趟排序的結(jié)果 
	}
}

int main()
{
	int a[8]={3,1,5,7,3,4,8,2};
	print(a,8,0);	// 打印原始序列 
	InsertSort(a,8);
	return 0;
}

分析：

時間復(fù)雜度：O（n^2）

插入排序——希爾排序（Shell Sort）

基本思想：

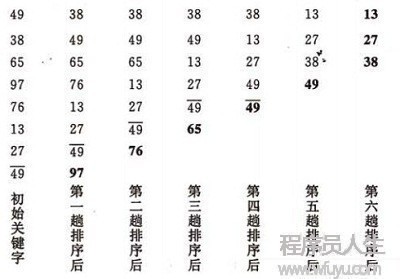
先將全部待排序的記錄序列分割成為若干子序列，分別進(jìn)行直接插入排序，待全部序列中的記錄“基本有序”時，再對全部記錄順次進(jìn)行直接插入排序。

操作方法：

選擇1個增量序列{ t1，t2，t3，...，tk }

按增量序列個數(shù)k，對序列進(jìn)行k趟排序；
每趟排序，根據(jù)對應(yīng)的增量ti，將待排序序列分割成若干長度為m的子序列，分別對各子序列進(jìn)行直接插入排序。僅增量由于為1時，全部序列作為1個整表來處理，表長度即為全部序列的長度。

希爾排序的示例：

算法實現(xiàn)：

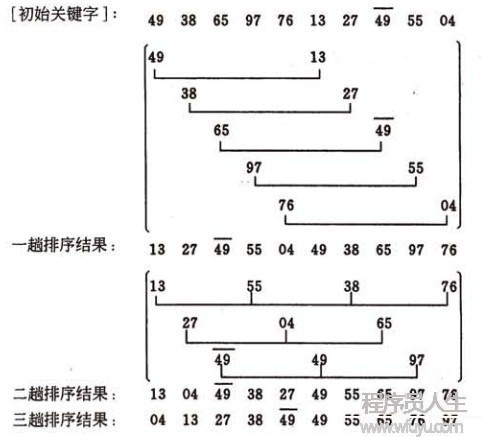
**如何選擇增量序列？

簡單選擇：增量序列d = { n/2，n/4，n/8，...，1 } ，其中n為要排序數(shù)的個數(shù)。

#include<iostream>
using namespace std;

void print(int a[], int n)
{   
    for(int j= 0; j<8; j++){  
        cout<<a[j] <<" ";  
    }  
    cout<<endl;  
}

void ShellInsertSort(int a[],int n,int dk)
{
	int i,j,tmp;
	for(i=dk;i<n;++i)
	{
		// 如果第i個元素大于第i-dk個元素，直接插入
		// 否則
		// 小于的話，移動有序表后插入 
		if(a[i]<a[i-dk])
		{
			j=i-dk;
			tmp=a[i];
			a[i]=a[i-dk]; // 復(fù)制哨兵，即存儲待排序元素
			while(tmp<a[j])
			{
				// 哨兵元素比插入點元素小，后移dk個元素
				a[j+dk]=a[j];
				j-=dk;
			}
			a[j+dk]=tmp; // 插入到正確的位置 
		}
	}
}

void ShellSort(int a[],int n)
{
	int dk=n/2;
	while(dk>=1)
	{
		ShellInsertSort(a,n,dk);
		dk/=2;
	}
}

int main()
{
	int a[8]={3,1,5,7,3,4,8,2};
	print(a,8);	// 打印原始序列 
	ShellSort(a,8);
	print(a,8); 	// 打印排序后的序列 
	return 0;
}

分析：

可以發(fā)現(xiàn)，希爾排序是對簡單插入排序算法的1種改進(jìn)。

但希爾排序是不穩(wěn)定的排序方法，由于排序進(jìn)程中可能會改變相同元素在原始序列中的前后關(guān)系。

關(guān)于希爾排序的時效分析，取決于增量因子序列d的選取，特定情況下可以估算出關(guān)鍵碼的比較次數(shù)和記錄的移動次數(shù)。

目前還沒有人給出選取最好的增量因子序列的方法。

選擇排序——簡單選擇排序（Simple Selection Sort）

基本思想：

在要排序的1組數(shù)中，選出最小（或最大）的1個數(shù)與第1個位置的數(shù)進(jìn)行交換；然后在剩下的數(shù)當(dāng)中再找最小（或最大）的數(shù)與第2個位置的數(shù)交換，順次類推，直到第n⑴個元素（倒數(shù)第2個數(shù)）和第n個元素（最后1個數(shù)）比較為止。

簡單選擇排序示例：

操作方法：

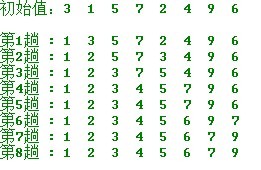
第1趟：從n個記錄中找出關(guān)鍵碼最小的記錄與第1個記錄交換；

第2趟：從第2個記錄開始的n⑴個記錄中再選出關(guān)鍵碼最小的記錄與第2個記錄交換；

以此類推...

第 i 趟：從第i個記錄開始的n-i+1個記錄當(dāng)選出關(guān)鍵碼最小的記錄與第i個記錄交換，直至全部序列按關(guān)鍵碼有序。

算法實現(xiàn)：

#include<iostream>
using namespace std;

void print(int a[], int n ,int i)
{  
    cout<<"第"<<i+1 <<"趟 : ";  
    for(int j= 0; j<8; j++){  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl;  
}

// 返回數(shù)組的最小值的鍵值
int SelectMinKey(int a[],int n,int i)
{
	int k=i;
	for(int j=i+1;j<n;++j)
		if(a[k]>a[j])
			k=j;
	return k;
}

void SelectSort(int a[],int n)
{
	int key,tmp;
	for(int i=0;i<n;++i)
	{
		key=SelectMinKey(a,n,i);	// 選擇最小的元素
		if(key!=i)
		{
			// 最小元素與第i位置元素互換 
			tmp=a[i];
			a[i]=a[key];
			a[key]=tmp;
		}
		print(a,n,i);
	}
}

int main()
{
	int a[8]={3,1,5,7,3,4,8,2};
	cout<<"原始序列：";
	for(int i=0;i<8;++i)
	{
		cout<<a[i];
		if(i==7)
			cout<<endl;
		else
			cout<<"  ";
	}
	SelectSort(a,8);
	return 0;
}

選擇排序——堆排序（Heap Sort）

基本思想：

1）初始化堆；將數(shù)列[ 1 ... n ]構(gòu)造成最大化堆

2）交換數(shù)據(jù)：將a[ 1 ]和a[ n ]交換，使a[ n ]是[ 1 ... n ]中的最大值；然后將[ 1 ... n⑴ ]重新調(diào)劑為最大堆。接著，將a[ 1 ]和a[ n⑴ ]交換，使a[ n⑴ ]是[ 1 ... n⑴ ]中的最大值；然后將[ 1 ... n⑵ ]重新調(diào)劑為最大堆。順次類推，直到全部數(shù)列有序。

堆排序的示例：

實現(xiàn)中用到了“數(shù)組實現(xiàn)的2叉堆的性質(zhì)”。

在第1個元素的索引為0的情形中：

性質(zhì)1：索引為i 的左孩子的索引是（2*i+1）；

性質(zhì)2：索引為i 的右孩子的索引是（2*i+2）；

性質(zhì)3：索引為i 的父節(jié)點的索引是floor( ( i⑴ ) / 2 )；

下面演示對a={20,30,90,40,70,110,60,10,100,50,80}, n=11進(jìn)行堆排序進(jìn)程

數(shù)組a對應(yīng)的初始結(jié)構(gòu)：

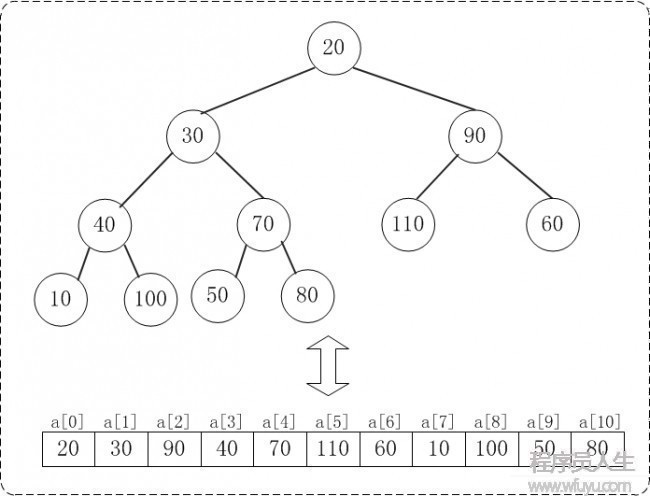
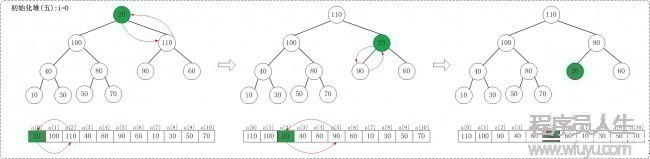
1 初始化堆：

在堆排序算法中，首先要將待排序的數(shù)組轉(zhuǎn)換成最大堆。

下面演示將數(shù)組{20,30,90,40,70,110,60,10,100,50,80}轉(zhuǎn)換為最大堆{110,100,90,40,80,20,60,10,30,50,70}的步驟。

1.1 i = n/2 - 1，即i = 4

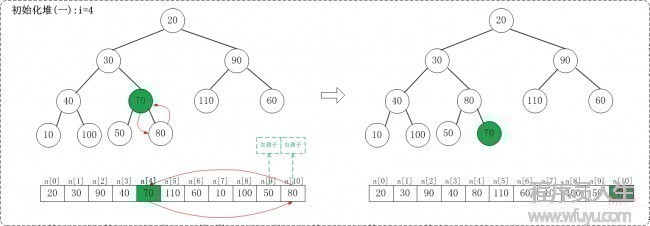
1.2 i = 3

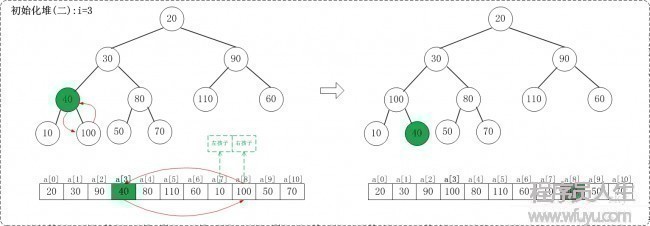
1.3 i = 2

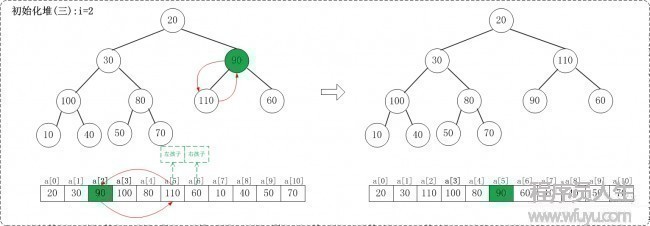
1.4 i = 1

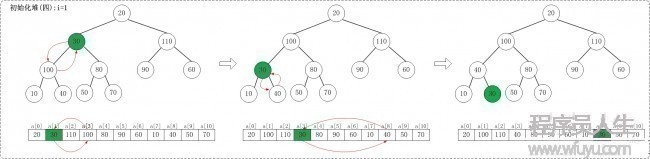
1.5 i = 0

2 交換數(shù)據(jù)

在將數(shù)組轉(zhuǎn)換成最大堆后，接著要進(jìn)行交換數(shù)據(jù)，從而使數(shù)組成為1個真實的有序數(shù)組。

下面是當(dāng)n = 10時交換數(shù)組的示意圖：

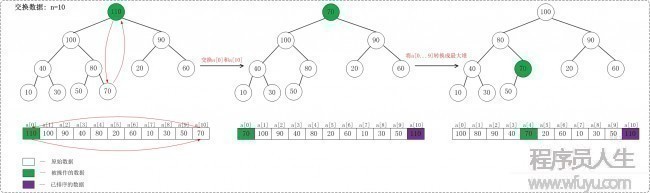
當(dāng)n = 10時，首先交換a[0]和a[10]，使得a[10]是a[0 ... 10 ]之間的最大值；然后調(diào)劑a[0 ... 9 ]使它成為最大堆。交換以后，a[10]是有序的；

當(dāng)n = 9時，首先交換a[0]和a[9]，使得a[9]是a[0 ... 9 ]之間的最大值；然后調(diào)劑a[0 ... 8 ]使它成為最大堆。交換以后，a[9]是有序的；

... ...

順次類推，直到a[0 ... 10 ]是有序的。

算法實現(xiàn)：

#include<iostream>
using namespace std;

void maxheap_down(int a[],int start,int end)
{
	int current=start;	// 當(dāng)前結(jié)點的位置
	int left=2*current+1;	// 左孩子的位置
	int tmp=a[current];	// 當(dāng)前節(jié)點的大小
	for(;left<=end;current=left,left=2*left+1)
	{
		if(left<end&&a[left]<a[left+1])
			++left;	// 左右孩子當(dāng)選擇較大者
		if(tmp>=a[left])
			break;	//調(diào)劑結(jié)束
		else
		{
			// 交換值
			a[current]=a[left];
			a[left]=tmp;
		} 
	} 
}

void HeapSort(int a[],int n)
{
	int i,tmp;
	// 從(n/2⑴) --> 0逐次遍歷。遍歷以后，得到的數(shù)組實際上是1個(最大)2叉堆。
	for(i=n/2⑴;i>=0;--i)
		maxheap_down(a,i,n⑴);
	// 從最后1個元素開始對序列進(jìn)行調(diào)劑，不斷的縮小調(diào)劑的范圍直到第1個元素
	for(i=n⑴;i>0;--i)
	{
		// 交換a[0]和a[i]。交換后，a[i]是a[0...i]中最大的
		tmp=a[i];
		a[i]=a[0];
		a[0]=tmp;
		// 調(diào)劑a[0...i⑴]，使得a[0...i⑴]依然是1個最大堆;
		// 即，保證a[i⑴]是a[0...i⑴]中的最大值
		maxheap_down(a,0,i⑴);
	}
}

int main()
{
	int i;
	int a[]={20,30,90,3,21,11,60,10,23,50,80};
	int len=(sizeof(a))/(sizeof(a[0]));
	cout<<"原始序列：";
	for(i=0;i<len;++i)
		cout<<a[i]<<" ";
	cout<<endl;
	HeapSort(a,len);
	cout<<"堆排序后的序列："; 
	for(i=0;i<len;++i)
		cout<<a[i]<<" ";
	cout<<endl;
	return 0;
}

分析：

時間復(fù)雜度：O（nlog2n）

遍歷1趟的時間復(fù)雜度是O（n）；

堆排序是采取2叉堆進(jìn)行排序的，2叉堆就是1棵2叉樹，它需要遍歷的次數(shù)就是2叉樹的深度，而根據(jù)完全2叉樹的定義，它的深度最少是log2(n+1)，最多也不會超過log22n。因此，遍歷次數(shù)介于log2(n+1)和log22n之間；因此得出它的時間復(fù)雜度是O（nlog2n）。

堆排序穩(wěn)定性：不穩(wěn)定的

它在交換數(shù)據(jù)的時候，是比較父節(jié)點和子節(jié)點之間的數(shù)據(jù)，所以即便是存在兩個數(shù)值相等的兄弟結(jié)點，它們的相對順序在排序中也可能產(chǎn)生變化。

交換排序——冒泡排序（Bubble Sort）

基本思想：

在要排序的1組數(shù)中，對當(dāng)前還未排好序的范圍內(nèi)的全部數(shù)，自上而下對相鄰的兩個數(shù)順次進(jìn)行比較和調(diào)劑，讓較大的數(shù)往下沉，較小的數(shù)往上冒。

即：每當(dāng)相鄰的數(shù)比較后發(fā)現(xiàn)它們的順序與排序要求相反時，就將它們互換。

冒泡排序的示例：

算法實現(xiàn)：

#include<iostream>
using namespace std;

void print(int a[], int n ,int i)
{  
    cout<<"第"<<i+1<<"趟 : ";  
    for(int j= 0; j<8; j++){  
        cout<<a[j]<<"  ";  
    }  
    cout<<endl;  
}

void BubbleSort(int r[],int size)
{
	int i,j,temp;
	bool exchange;	//交換標(biāo)志
	for(i=0;i<size;i++)
	{
		exchange=false;	//本趟排序開始前，交換標(biāo)志設(shè)為假
		for(j=size⑴;j>=i;--j)
			if(r[j]<r[j⑴])
			{
				temp=r[j];	//暫存單元 
				r[j]=r[j⑴];
				r[j⑴]=temp;
				exchange=true;	//產(chǎn)生了交換，故將交換標(biāo)志置為真 
			}
		if(!exchange)	//本趟沒有產(chǎn)生交換，提早終止算法 
			return;
		print(r,size,i);
	}
}

int main()
{
	int r[8]={3,1,5,7,3,4,8,2};
	cout<<"原始序列：";
	for(int i=0;i<8;i++)
	{
		cout<<r[i];
		if(i==7)
			cout<<endl;
		else
			cout<<"  ";
	}
	BubbleSort(r,8);
	return 0;
}

交換排序——快速排序（Quick Sort）

基本思想：

1）選擇1個基準(zhǔn)元素，通常選擇第1個元素或最后1個元素

2）通過1趟排序?qū)⒋判虻挠涗浄指畛瑟毩⒌膬刹糠荩渲?部份記錄的元素值均比基準(zhǔn)元素值小，另外一部份記錄的元素值比基準(zhǔn)值大。

3）此時基準(zhǔn)元素在其排好序后的正確位置

4）然后分別對這兩部份記錄用一樣的方法繼續(xù)進(jìn)行排序，直到全部序列有序

快速排序的示例：

a）1趟排序的進(jìn)程：

b）排序的全進(jìn)程：

算法實現(xiàn)：

#include<iostream>
using namespace std;

int Partition(int r[],int first,int end)
{
	int i=first,j=end,temp;	//初始化
	while(i<j)
	{
		//j從后向前掃描，直到r[j]<r[i]，將r[j]移動到r[i]的位置，使關(guān)鍵碼小（同軸值相比）的記錄移動到前面去；
		while(i<j && r[i]<=r[j]) --j;	//右邊掃描
		if(i<j)
		{
			//將較小記錄交換到前面
			temp=r[i];
			r[i]=r[j];
			r[j]=temp;
			++i;
		}
		//i從前向后掃描，直到r[i]>r[j]，將r[i]移動到r[j]的位置，使關(guān)鍵碼大（同軸值相比）的記錄移動到后面去；
		while(i<j && r[i]<=r[j]) ++i;	//左邊掃描
		if(i<j)
		{
			//將較大記錄交換到后面
			temp=r[i];
			r[i]=r[j];
			r[j]=temp;
			--j;
		}
		//重復(fù)上述進(jìn)程，直到i=j
	}
	return i;
}

void QuickSort(int r[],int first,int end)
{
	if(first<end)
	{
		int pivotpos=Partition(r,first,end);	//1次劃分
		QuickSort(r,first,pivotpos⑴);	//對前1個子序列進(jìn)行快速排序
		QuickSort(r,pivotpos+1,end);	//對后1個子序列進(jìn)行快速排序
	}
	
}

int main()
{
	int r[8]={3,1,5,7,3,4,8,2};
	cout<<"原始序列：";
	for(int i=0;i<8;i++)
	{
		cout<<r[i];
		if(i==7)
			cout<<endl;
		else
			cout<<"  ";
	}
	QuickSort(r,0,7);
	cout<<"排序后的序列：";
	for(int i=0;i<8;i++)
	{
		cout<<r[i];
		if(i==7)
			cout<<endl;
		else
			cout<<"  ";
	}
	return 0;
}

分析：

快速排序通常被認(rèn)為在同數(shù)量級（O（nlog2n）中平均性能最好的。但如果初始序列按關(guān)鍵碼有序或基本有序時，快速排序反而退化為冒泡排序。

為改進(jìn)之，通常以“3者取中法“來選取基準(zhǔn)記錄，行將排序區(qū)間的兩個端點與中點3個記錄關(guān)鍵碼居中地調(diào)劑為支點記錄。

快速排序是1個不穩(wěn)定的排序算法。

歸并排序（Merge Sort）

基本思想：

歸并排序是將兩個（或兩個以上）的有序表合并成1個新的有序表，行將待排序序列分為若干個子序列，每一個序列是有序的。然后再將有序子序列合并為整體有序序列。

歸并排序示例：

合并方法：

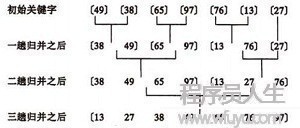
1個元素的表總是有序的，所以對n個元素的待排序列，每一個元素可看成1個有序子表。對子表兩兩合并，生成n/2個子表，所得子表除最后1個子表長度可能為1外，其余子表長度均為2。再進(jìn)行兩兩合并，直到生成n個元素按關(guān)鍵碼有序的表。

算法實現(xiàn)：

#include<iostream>
using namespace std;
 
void print(int a[], int n)
{  
    for(int j=0; j<n; j++){  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl;  
} 

void merge(int r[],int left,int mid,int right)
{
	int *rf=new int[right-left+1];	//匯總2個有序區(qū)的臨時數(shù)組 
	int i=left;		 // 第1個有序區(qū)的索引
	int j=mid+1;	 // 第2個有序區(qū)的索引
	int k=0;		// 臨時區(qū)域的索引
	while(i<=mid&&j<=right)
	{
		if(r[i]<r[j])
		{
			rf[k++]=r[i++];
		}
		else
		{
			rf[k++]=r[j++];
		} 
	} 
	while(i<=mid)
		rf[k++]=r[i++];
	while(j<=right)
		rf[k++]=r[j++];
	// 將排序后的元素，全部都整合到數(shù)組a中。
    for(i=0;i<k;i++)
        r[left + i] = rf[i];
	delete []rf;
}

void MergeSort(int r[],int left,int right)
{
	if(r!=NULL&&left<right)
	{
		int mid=(left+right)/2;
		MergeSort(r,left,mid);		// 遞歸排序a[start...mid]
		MergeSort(r,mid+1,right);	// 遞歸排序a[mid+1...end]
		// a[start...mid] 和 a[mid...end]是兩個有序空間，
    	// 將它們排序成1個有序空間a[start...end]
		merge(r,left,mid,right);
	}
} 

int main()
{
	int r[9]={32, 21, 67, 11, 5, 43, 99, 18,12};
	cout<<"原始序列：";
	print(r,9);
	MergeSort(r,0,8);
	cout<<"歸并排序后的序列：";
	print(r,9);
	return 0;
}

分析：

歸并排序的時間復(fù)雜度是O（nlog2n）

歸并排序的情勢就是1顆2叉樹，它需要遍歷的次數(shù)就是2叉樹的深度，而根據(jù)完全2叉樹的深度可以得出它的時間復(fù)雜度是O（nlog2n）。

歸并排序是穩(wěn)定的算法，它滿足穩(wěn)定算法的定義。

桶排序/基數(shù)排序（Radix Sort）

基本思想：

將數(shù)組分到有限數(shù)量的桶子里；

假定待排序的數(shù)組a中共有n個整數(shù)，并且已知數(shù)組a中的數(shù)據(jù)大小范圍是[ 0 , MAX ) 。在桶排序時，創(chuàng)建容量為MAX的桶數(shù)組r，并將桶數(shù)組的元素都初始化為0；將容量為MAX的桶數(shù)組中的每個單元都看成1個“桶”。

在排序時，逐一遍歷數(shù)組a，將數(shù)組a的值作為“桶數(shù)組r”的下標(biāo)。當(dāng)a中的數(shù)據(jù)被讀取時，就將相應(yīng)的桶的值加1。例如，讀取到數(shù)組a[3]=5，就將r[5]的值+1。

桶排序的示例：

假定a={8,2,3,4,3,6,6,3,9}, max=10。此時，將數(shù)組a的所有數(shù)據(jù)都放到需要為0⑼的桶中。以下圖：

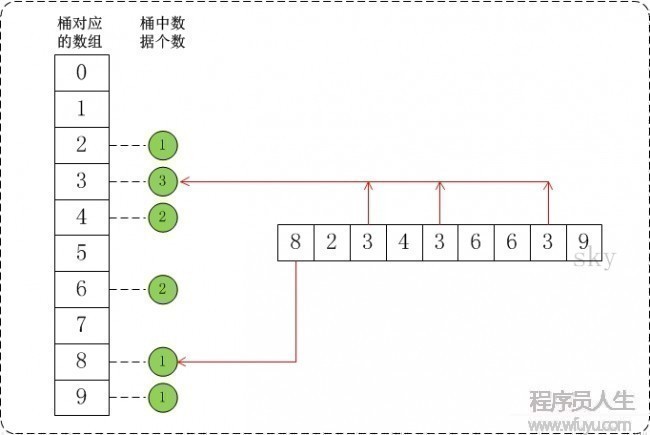
在將數(shù)據(jù)放到桶中以后，再通過1定算法將桶中的數(shù)據(jù)提出來并轉(zhuǎn)換成有序數(shù)組，這就得到我們需要的有序序列。

算法實現(xiàn)：

#include<iostream>
#include<cstring>	// memset頭文件 
using namespace std;

void BucketSort(int a[],int n,int max)
{
	int i,j;
	int buckets[max];
	// 將buckets中的所有數(shù)據(jù)都初始化為0
	memset(buckets,0,max*sizeof(int));
	// 計數(shù)
	for(i=0;i<n;++i)
		++buckets[a[i]]; 
	// 排序
	for(i=0,j=0;i<max;++i)
		while((buckets[i]--)>0)
			a[j++]=i;
}

int main()
{
	int i;
    int a[] = {8,2,1,4,3,7,6,3,9};
    int len = (sizeof(a))/(sizeof(a[0]));
    cout<<"原始序列：";
	for(i=0;i<len;++i)
		cout<<a[i]<<" ";
	cout<<endl;
	BucketSort(a,len,10);
	cout<<"堆排序后的序列："; 
	for(i=0;i<len;++i)
		cout<<a[i]<<" ";
	cout<<endl;
	return 0;
}

—————————————————————————————————————————————————————————————————————————————

總結(jié)

各種排序的穩(wěn)定性，時間復(fù)雜度和空間復(fù)雜度總結(jié)：

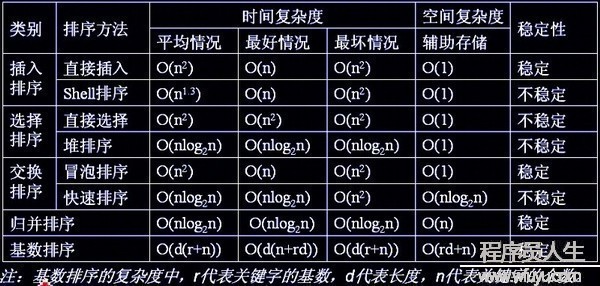
對n較大的排序記錄。1般的選擇都是時間復(fù)雜度為O(nlog2n)的排序方法。

生活不易，碼農(nóng)辛苦
如果您覺得本網(wǎng)站對您的學(xué)習(xí)有所幫助,可以手機(jī)掃描二維碼進(jìn)行捐贈
程序員人生

------分隔線----------------------------

上一篇 docker的devicemapper存儲驅(qū)動

下一篇 CSS3制作3D水晶糖果按鈕

分享到:

------分隔線----------------------------

汐顏

積分：3341

6粉絲

0關(guān)注

欄目熱點

多多色-多人伦交性欧美在线观看-多人伦精品一区二区三区视频-多色视频-免费黄色视屏网站-免费黄色在线

數(shù)據(jù)結(jié)構(gòu)--排序算法總結(jié)

概述

插入排序——直接插入排序（Straight Insertion Sort）

基本思想：

直接插入排序示例：

算法實現(xiàn)：

分析：

插入排序——希爾排序（Shell Sort）

基本思想：

操作方法：

希爾排序的示例：

算法實現(xiàn)：

分析：

選擇排序——簡單選擇排序（Simple Selection Sort）

基本思想：

簡單選擇排序示例：

操作方法：

算法實現(xiàn)：

選擇排序——堆排序（Heap Sort）

基本思想：

堆排序的示例：

算法實現(xiàn)：

分析：

交換排序——冒泡排序（Bubble Sort）

基本思想：

冒泡排序的示例：

算法實現(xiàn)：

交換排序——快速排序（Quick Sort）

基本思想：

快速排序的示例：

算法實現(xiàn)：

分析：

歸并排序（Merge Sort）

基本思想：

歸并排序示例：

合并方法：

算法實現(xiàn)：

分析：

桶排序/基數(shù)排序（Radix Sort）

基本思想：

桶排序的示例：

算法實現(xiàn)：

總結(jié)