您當前位置：首頁 > php開源 > php教程 > 數據結構學習筆記（一）：基本概念：什么是數據結構和算法，應用實例

數據結構學習筆記（一）：基本概念：什么是數據結構和算法，應用實例

來源：程序員人生發布時間：2016-12-12 15:02:33 閱讀次數：3005次

前言

由于要開始實習了，發現之前有些學過的東西。哪怕是我曾花了很大的力氣學過的，由于長時間的沒有被使用。致使很多知識都忘記了。所以準備在投簡歷面試前，把知識全部鞏固1下。

在中國大學MOOC（慕課）網上，準備開始學習浙江大學的數據結構，由陳越、何欽銘老師主講。（講的非常好）

課程地址：
http://www.icourse163.org/learn/ZJU⑼3001?tid=1001757011#/learn/announce

基本概念

1.1 甚么是數據結構

數據結構并沒有官方的定義。

1般來講，我們通常描寫“數據結構”的時候，總會帶著“算法”1詞，因而可知數據結構必定是跟算法相干的。

老師提了個小問題。

1.1.1 關于數據組織—例1：圖書擺放

例1：如果我給你1些書，和1些存儲這些書的空間，你要怎樣存儲這些書呢？

這里寫圖片描述

我選的是A（我當時1秒就覺得隨意放啊。沒斟酌那末多。。這其實也說明了，如果在處理問題之前，就沒有1個比較完善的解決方案的話，那末真正遇到問題，就真的1臉懵逼了，大家不要學我TVT）

正確答案是。。

由于老師并沒有告知我們書架的范圍，而不1樣范圍的數據，數據組織的情勢也不同。

難不是在于如何放書，而是在于放這個書如何使：插入（放新書）和查詢書，這兩個操作更方便

方法1：隨意放（放簡單了，查詢累死），如果是小范圍的書，2本，無所謂。大范圍，就不行。

方法2：依照書名的拼音順序排放（查找容易，插入難，由于要給書挪位）

方法3：把書架劃分成幾塊區域，每塊區域指定放某種種別的圖書；在某種種別內，依照書名的拼音字母順序排放

插入：先定種別，2分查找肯定位置，移出空位
查找書：先定種別，再2分查找

不過此時就有新的問題。如何劃分種別（分多細好呢？分細很難找，分少了也不行）和每一個種別所占的位置（少了就又要挪位，多了又浪費）

這個小故事告知我們：解決問題方法的效力，跟數據組織的方式是直接相干的（這就是數據結構的意義所在）

關于空間使用—例2：PrintN函數的實現

例2：寫程序實現1個函數PrintN，使得傳入1個正整數為N的參數后，能順序打印從1到N的全部正整數。

給兩個代碼

//代碼1
void PrintN(int N)
{
int i;
    for(i=1;i<=N;i++)
    {
        printf("%d\n",i);
    }
    reutrn;
}

//代碼2
void PrintN(int N)
{
    if(N)
    {
        printN(N-1);
        printf("%d\n",N);
    }
    return;
}

代碼1和代碼2初看之下，代碼量差不多。

1是用循環實現的，2是用遞歸實現的。

而遞歸函數連臨時變量都沒有用（代碼1中的臨時變量i），令人容易理解，看起來簡單明了。

那末兩個代碼。運行效力如何呢？

當N=10，100，1000，10000，100000（10萬）時的區分

建議大家實驗下，N=10和N=10萬的時候

（N=10萬的時候，遞歸函數罷工了，沒有出正確結果）

結論：遞歸函數對電腦的空間占用是非常恐怖的，對善于寫遞歸函數的人來講，遞歸函數簡單明了，對計算機來講，它非常吃內存，效力低。

也說明了解決問題方法的效力，跟空間的利用效力有關（還記得例題1得到的結論么（溫習1下）：解決問題方法的效力，跟數據組織的方式是直接相干的

1.1.3 關于算法效力—例3：計算多項式的值

例：寫程序計算給定多項式在給定點x處的值

多項式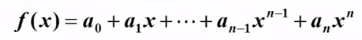：這里寫圖片描述

//代碼1
double f(int n,double a[],double x)
{
    int i;
    double p=a[0];
    for(i=1;i<=n;i++)
        p+=(a[i]*pow(x,i));
    return p;
}

聰明的我們，應當先對多項式提取公因子進行處理

處理后的多項式：
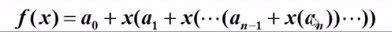
這里寫圖片描述

//代碼2
double f(int n,double a[],double x)
{
    int i;
    double p=a[n];
    for(i=n;i>0;i--)
        p=a[i-1]+x*p;
    return p;
}

想要知道哪一個方法效力高。

C語言中提供了1個函數：

clock()：捕捉從程序開始運行到clock()被調用時所耗費的時間。這個時間單位是clock tick，即“時鐘打點”。

常數CLK_TCK：機器時鐘每秒所走的時鐘打點數。

經常使用模板：

#include<stdio.h>
#include<time.h>

//clock_t是clock()函數返回的變量類型
clock_t start,stop;

//記錄被測函數運行時間，以秒為單位
double duration;

int main()
{
    //不在測試范圍的準備工作寫在clock()調用之前
    start=clock();   //開始計時
    MyFunction();    //把被測函數加在這里
    stop=clock();    //停止計時
    duration=((double)(stop-start))/CLK_TCK;  //計算運行時間

    //其他不在測試范圍的處理寫在后面，例如輸出duration的值
    return 0;
}

例3：寫程序計算給定多項式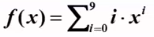這里寫圖片描述在給定點x=1.1處的值f(1.1)

//代碼1

#include<math.h>  //由于使用了pow函數
double f(int n,double a[],double x)
{
    int i;
    double p=a[0];
    for(i=1;i<=n;i++)
        p+=(a[i]*pow(x,i));
    return p;
}

//代碼2
double f(int n,double a[],double x)
{
    int i;
    double p=a[n];
    for(i=n;i>0;i--)
        p=a[i-1]+x*p;
    return p;
}

不過這兩個函數由于運行時間都太快了。。不到1秒。。那末如何測呢？

重復

讓被測函數重復運行屢次，使得測出的總的時鐘打點間隔充分長，最后計算被測函數平均每次運行的時間便可

1.1.4 抽象數據類型—例4：“矩陣”的抽象數據類型定義

到底甚么是數據結構？

數據對象在計算機中的組織方式（像前面提的放書問題）
- 邏輯結構（如果1開始將書架想象成1條挨在1起的長架子，這樣就是線性結構，1對1的；如果是將圖書分類，那末1個類里面就會有很多書，這樣是對多的，這樣就是樹型結構；如果我們需要統計，這本書被哪些人買過，買了這本書的人還買過哪些書，因而就是1本書對應很多人，那末1個人又對應很多書，所以這就是個很復雜的關系結構，叫做圖結構）
- 物理存儲結構（我們說的邏輯結構到底在計算機里如何存儲）
數據對象一定與1系列加在其上的操作相干聯
完成這些操作所用的方法就是算法

描寫數據結構，我們通常使用抽象數據類型進行描寫

抽象數據類型：

數據類型
- 數據對象集
- 數據集合相干聯的操作集（這兩個東西在C語言是分開處理的，但是在高級語言里，如JAVA，C++，以類的情勢將它們封裝在1起）
抽象：描寫數據類型的方法不依賴于具體實現
- 與寄存數據的機器無關
- 與數據存儲的物理結構無關
- 與實現操作的算法和編程語言均無關

只描寫數據對象集合相干操作集“是甚么”，其實不觸及“如何做到”的問題

例4：“矩陣”的抽象數據類型定義

這里寫圖片描述

1.2 甚么是算法

1.2.1 算法的定義—例1：選擇排序算法的偽碼描寫

算法（Algorithm）

1個有限指令集
接受1些輸入（有些情況下不需要輸入）
產生輸出
1定在有限步驟以后終止
每條指令必須
- 有充分明確的目標，不可以有歧義
- 計算性能處理的范圍以內
- 描寫應不依賴于任何1種計算機語言和具體的實現手段

例1：選擇排序算法的偽碼描寫

//選擇排序算法的偽碼描寫

void SelectionSort(int List[],int N)
{
    //將N個整數List[0]...List[N⑴]進行非遞減排序
    for(i=0;i<N;i++)
    {
        //從List[i]到List[N⑴]中找最小元，并將其位置賦給MinPositon
        MinPositon=ScanForMin(List,i,N-1);
        //將未排序部份得最小元換到有序部份的最后位置
        Swap(List[i],List[MinPositon]);
    }
}

1.2.2 甚么是好的算法？

空間復雜度S(n)—-根據算法寫成的程序在履行時占用存儲單元的長度。這個長度常常與輸入數據的范圍有關。空間復雜度太高的算法可能致使使用的內存超限，造成程序非正常中斷（前面的例2中的代碼2使用的遞歸，傳10萬時）
時間復雜度T(n)—-根據算法寫成的程序在履行時耗費時間的長度。這個長度常常也與輸入數據的范圍有關。時間復雜度太高的低效算法可能致使我們在有生之年都等不到運行結果（前面例3中代碼1的時間復雜度為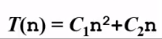，代碼2的時間復雜度為）

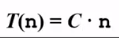在分析1般算法的效力時，我們常常關注下面兩種復雜度
這里寫圖片描述

1.2.3 復雜度的漸進表示

復雜度的漸進表示法

這里寫圖片描述

經常使用復雜度函數

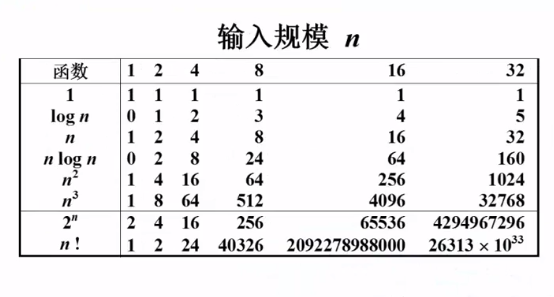
這里寫圖片描述

經常使用復雜度函數圖表表示
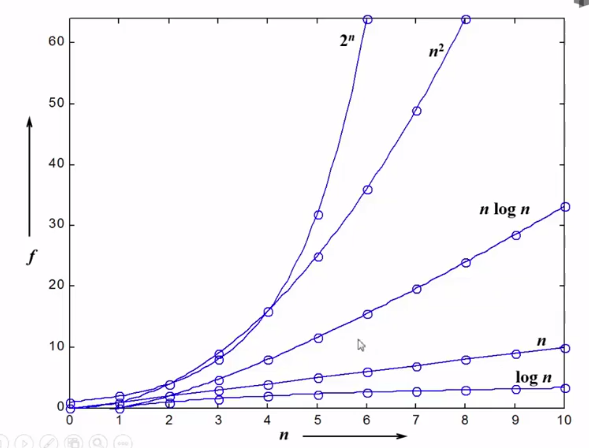
這里寫圖片描述

復雜度分析小訣竅

這里寫圖片描述

1.3 利用實例：最大子列和問題

1.3.1 利用實例—算法1&2

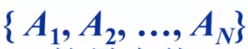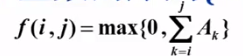問題：給定N個整數的序列這里寫圖片描述，求函數的最大值。
（不懂子列的意思的，可以想象成子集，比如說{A,B,C}，那末子列就有{A，}{B}，{C}，{A,B}，{A,C}，{B,C}，{A,B,C}，求最大子列和相當于最大自己包括的元素數。這個例題中最大的元素數為3）
算法1：

//算法1：暴力求出所有子列和，再找出最大的

int MaxSubseqSum1(int A[],int N)
{
    int ThisSum,MaxSum=0;
    int i,j,k;
    for(i=0;i<N;i++)       //i是子列左端位置
    {
        for(j=i;j<N;j++)   //j是子列右端位置
        {
            ThisSum=0;     //ThisSum是從A[i]到A[j]的子列和
            for(k=i;k<=j;k++)
                ThisSum+=A[k];
            if(ThisSum>MaxSum)  //如果剛得到的這個子列和更大，則更新結果
                MaxSum=ThisSum;

        }//j循環結束
    }    //i循環結束
    return MaxSum;
}

算法2：

//算法2
int MaxSubseqSum2(int A[],int N)
{
    int ThisSum,MaxSum=0;
    int i,j;
    for(i=0;i<N;i++)       //i是子列左端位置
    {
        ThisSum=0;         //ThisSum是從A[i]到A[j]的子列和
        for(j=i;j<N;j++)   //j是子列右端位置
        {
            ThisSum+=A[j]; //對不同的i,不同的j，只要在j⑴次循環的基礎上累加1項便可
            if(ThisSum>MaxSum) //如果剛得到的子列和更大，則更新結果
                MaxSum=ThisSum;
        }//j循環結束
    }    //i循環結束
    return MaxSum;  
}

1.3.2 利用實例—算法3：分而治之

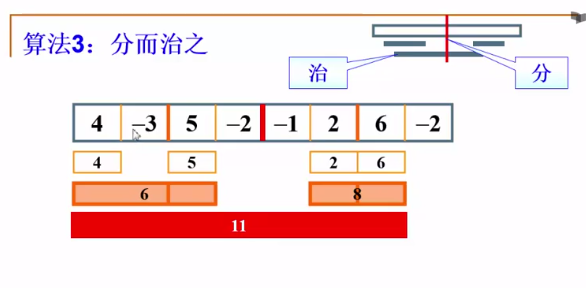
算法3：

分而治之可以將1個序列從中間分為2個，可能最大子序列就是這兩個被分開當中最大的。也有可能正好逾越了兩個。

這里寫圖片描述

int Max3( int A, int B, int C )
{ 
    /* 返回3個整數中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}

int DivideAndConquer( int List[], int left, int right )
{ 
    /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 寄存左右子問題的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*寄存跨分界限的結果*/

    int LeftBorderSum, RightBorderSum;
    int center, i;

    if( left == right )  
    {  
        /* 遞歸的終止條件，子列只有1個數字 */
        if( List[left] > 0 )  
            return List[left];
        else 
            return 0;
    }

    /* 下面是"分"的進程 */
    center = ( left + right ) / 2; /* 找到中分點 */

    /* 遞歸求得兩邊子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );

    /* 下面求跨分界限的最大子列和 */
    MaxLeftBorderSum = 0;  
    LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) 
    { 
        /* 從中線向左掃描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左側掃描結束 */

    MaxRightBorderSum = 0; 
    RightBorderSum = 0;
    for( i=center+1; i<=right; i++ )
    { 
        /* 從中線向右掃描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右側掃描結束 */

    /* 下面返回"治"的結果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}

int MaxSubseqSum3( int List[], int N )
{ 
    /* 保持與前2種算法相同的函數接口 */
    return DivideAndConquer( List, 0, N-1 );
}

1.3.3 利用實例—算法4：在線處理

算法4：在線處理

//算法4（在線處理）的偽碼描寫

int MaxSubseqSum4(int A[],int N)
{
    int ThisSum,MaxSum;
    int i;
    ThisSum=MaxSum=0;
    for(i=0;i<N;i++)
    {
        ThisSum+=A[i];       //向右累加
        if(ThisSum>MaxSum)
            MaxSum=ThisSum;  //發現更大的則更新當前結果
        else if(ThisSum<0)   //如果當前子列和為負
            ThisSum=0;       //則不可能使后面的部份和增大，拋棄之
    }
    return MaxSum;
}