013--Floyd算法-動態規劃-《算法設計技巧與分析》M.H.A學習筆記
來源:程序員人生 發布時間:2016-07-07 13:57:46 閱讀次數:2422次
多源最短路:有向圖,求從每一個頂點到其他所有頂點的最短距離。
基本思路:
假定有向圖的所有點編號為1到n,l[i,j]表示從i到j的邊的長度,如果不存在邊,則置為正無窮。
定義d(k,i,j)表示從點i到點j,并且不經過編號大于k的點的最短距離。
初始化條件:
K=0時,d(0,i,j)=l[i,j]。
狀態轉移方程:
d(k,i,j)=min{ d(k⑴,i,j),d(k⑴,i,k)+d(k⑴,k,j) } 1<=k<=n
因而我們有以下的遞歸式:
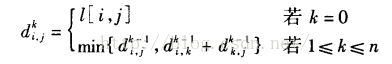
算法分析:
明顯,Floyd算法的時間復雜度是Θ(n3),空間復雜度是Θ(n2)。
偽代碼:


C++代碼:
for( int k = 1; k <= n; ++k )
for( int i = 1; i <= n; ++i )
for( int j = 1; j <= n; ++j )
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈