splay的原名是舒展樹，1種超級實用的數(shù)據(jù)結(jié)構(gòu)，能快速地干很多數(shù)據(jù)結(jié)構(gòu)不能干的事情。
很久之前就聽說過并且稍微地學(xué)了1些，但是當(dāng)時了解地其實不是很多。
有些人把splay達(dá)成spaly叫做死吧你，(⊙﹏⊙)b
實質(zhì)上他是1個2叉搜索樹，就是每一個節(jié)點的左兒子在原序列中是在自己左側(cè)的，右兒子在原序列中是在自己右側(cè)的，構(gòu)圖的方式有很多。
每個節(jié)點都可以存儲1些值，表示它的子樹中的信息（比如說甚么最大值啊，和啊以內(nèi)的）。
fo(i,1,n){
scanf("%d",&a[i+1]);f[i]=i+1;
t[i+1][0]=i;update(i+1);
}
f[n+1]=root=n+2,t[n+2][0]=n+1;update(n+2);初學(xué)者的構(gòu)圖可以構(gòu)成1條鏈。這樣很明顯左兒子在原序列上的位置是在自己左側(cè)的了。
但是有1個很奇妙的問題，為何從2號點開始建？為何建完點還要再向上多開1個n+2號點？
其實這類打法可以免后面的特判，現(xiàn)在的1號點和n+2號點是建立在首尾兩段的，如果不建立這兩個點2號點的兒子和n+1號點的父親都會指向0并傳遞信息，但是首尾建立1個虛點在修改操作中可以更方便的操作。比如說旋轉(zhuǎn)的時候要觸及到首尾的時候，如果沒有虛點，沒法把首尾單獨(dú)放到1個子樹中去。
其實建成1條鏈在后面的操作會很慢。
int build(int l,int r,int y){
if(l>r)return 0;
int mid=(l+r)/2;
int x=insert(a[mid]);f[x]=y;
if(l==r)return x;
tt[x][0]=build(l,mid-1,x);
tt[x][1]=build(mid+1,r,x);
update(x);
return x;
}
root=build(0,n+1,0);insert是建點操作，到后面再講。
這樣1開始就建成1顆2叉樹會比較快。
首先講1個重要的部份，就是旋轉(zhuǎn)。
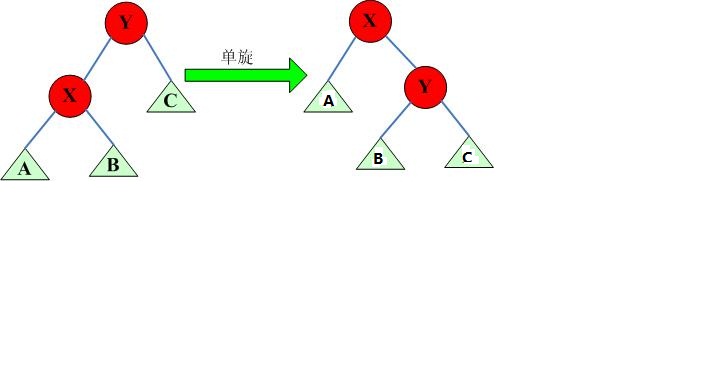
其實splay這顆2叉樹的中序遍歷就是原序列，例如圖中的原序列就是：AXBYC。現(xiàn)在我們要把x旋轉(zhuǎn)到y(tǒng)的位置上，但是不能改變這棵樹的中序遍歷（及在原序列的前后順序）。
bool son(int x){
if(tt[f[x]][0]==x)return 0;return 1;
}
void rotate(int x){
int y=f[x],z=son(x);
tt[y][z]=tt[x][1-z];
if(tt[x][1-z])f[tt[x][1-z]]=y;f[x]=f[y];
if(f[y])tt[f[y]][son(y)]=x;
f[y]=x;tt[x][1-z]=y;
update(y);update(x);
}其實代碼很短(f[x]表示x的父親，tt[x][0]和tt[x][1]分別是x的左右兒子)。
函數(shù)son(x)的作用是分辨x是其父親的左兒子還是右兒子(左兒子是0，右兒子是1)。
當(dāng)把x旋轉(zhuǎn)到y(tǒng)是，y就成為的x的右兒子，但是x原來的右兒子B就沒有地方放了。怎樣辦？我們發(fā)現(xiàn)在原序列中的順序是X < B < Y， 所以B應(yīng)當(dāng)在X的右側(cè)但是在Y的左側(cè)，所以現(xiàn)在Y的左兒子應(yīng)當(dāng)是B右兒子不變。如圖所示。
代碼應(yīng)用了1個小技能z和1-z恰好把0和1轉(zhuǎn)化，也能夠打成z和z^1（^是xor，異或）。
void splay(int x,int y){
if(x==y)return;
remove(x,y);
while(f[x]!=y){
if(f[f[x]]!=y)if(son(f[x])==son(x))rotate(f[x]);else rotate(x);
rotate(x);
}
if(!y)root=x;
}remove是懶標(biāo)記下傳，后面再講。
為何是把x旋轉(zhuǎn)為y的兒子，由于這樣更加方便的操作，比如說要對x的子樹進(jìn)行操作，如果變成把x旋轉(zhuǎn)到y(tǒng)的位置會麻煩很多而且不方便打。
旋轉(zhuǎn)的思路：如果x和x的父親和x的爺爺是1條折線，那末就旋轉(zhuǎn)成不是1個折線，然后像上面將的旋轉(zhuǎn)1樣向上推動。具體的最好自己畫個圖，有益于理解。
1般像splay(x,0)就是把x旋轉(zhuǎn)為根節(jié)點，splay(x,y)就是把x旋轉(zhuǎn)為y的兒子(具體是左兒子還是有兒子根據(jù)原序列中的順序來定)
void update(int x){
if(!x)return;
t[x].size=1+t[tt[x][0]].size+t[tt[x][1]].size;
t[x].sum=key[x]+t[tt[x][0]].sum+t[tt[x][1]].sum;
t[x].lda=max(t[tt[x][0]].lda,t[tt[x][0]].sum+key[x]+t[tt[x][1]].lda);
t[x].rda=max(t[tt[x][1]].rda,t[tt[x][1]].sum+key[x]+t[tt[x][0]].rda);
t[x].mx=max(max(t[tt[x][0]].mx,t[tt[x][1]].mx),t[tt[x][0]].rda+t[tt[x][1]].lda+key[x]);
}當(dāng)x節(jié)點的子節(jié)點變動是就需要更新，具體更新的內(nèi)容據(jù)題目而定。
x=kth(root,l-1);splay(x,0);
y=kth(root,r+1);splay(y,x);如果要對[l,r]這段區(qū)間進(jìn)行操作。思路：先把這段區(qū)間同時放到1顆子樹上去且這可子樹沒有其他過剩的節(jié)點。
首先如果把l⑴旋轉(zhuǎn)成根節(jié)點，那末[l,n]的節(jié)點都會在l⑴(及root)的左子樹上。然后再把r+1旋轉(zhuǎn)為l⑴的兒子，由于r+1在序列中再l⑴的右側(cè)，所以r+1旋轉(zhuǎn)以后1定是l⑴的右兒子，那末在原序列中的順序大于l⑴的，小于r+11定都是現(xiàn)在r+1節(jié)點的左子樹了。
那末現(xiàn)在只要對r+1的左子樹進(jìn)行操作就行了。
printf("%d\n",t[tt[y][0]].mx);比如要輸出[l,r]段的最大值，上段程序后面只用加上這段程序就能夠了。
現(xiàn)在要把a(bǔ)數(shù)組中的數(shù)從posi位置后開始插入進(jìn)序列中。
參照對1段節(jié)點進(jìn)行操作。
fo(i,1,k)scanf("%d",&a[i]);
x=kth(root,posi);splay(x,0);
y=kth(root,posi+1);splay(y,x);
tt[y][0]=build(1,k,y);現(xiàn)在只需要把這k個數(shù)插進(jìn)y的左子樹中就能夠了。build就是上面構(gòu)圖中的build，實質(zhì)就是把a(bǔ)數(shù)組1到k中的節(jié)點插為y的子樹。
現(xiàn)在要從posi這個位置開始刪去k個節(jié)點。
參照對1段節(jié)點進(jìn)行操作。
scanf("%d%d",&posi,&k);posi++;
x=kth(root,posi⑴);splay(x,0);
y=kth(root,posi+k);splay(y,x);
del(tt[y][0]);
tt[y][0]=0;
update(y);update(x);這里也同理，由于要從posi開始刪節(jié)點，序列的位置要比posi⑴大，比posi+k小。
del函數(shù)是甚么呢？
void del(int x){
if(!x)return;
shan[++shan[0]]=x;
del(tt[x][0]);del(tt[x][1]);
}由于刪去了1些點，這些點原來的位置不能浪費(fèi)在那里，用1個棧存起來，建點的以后再用。
int insert(int x){
int o;
if(shan[0])o=shan[shan[0]--];else o=++num;//主要是這行
初始化
.例如:key[o]=t[o].sum=t[o].mx=x;t[o].size=1;根據(jù)題目而定
.
.
}為了避免空間的浪費(fèi)，如果還有刪除過得節(jié)點的位置空在那里的話，就調(diào)用出來，否則就新建1個位置。
例如從posi開始后的k個點都加上k，參照對1段節(jié)點進(jìn)行操作。
x=kth(root,posi⑴);splay(x,0);
y=kth(root,posi+k);splay(y,x);
change(tt[y][0],zhi);
update(y);update(x);同理。
void change(int x,int y){//這里打的是區(qū)間加操作，據(jù)題目而定
if(!x)return;
t[x].sum+=t[x].size*y;
key[x]+=y;t[x].add+=y;//add是懶標(biāo)記，用于標(biāo)記下傳
if(y>0)t[x].lda=t[x].rda=t[x].mx=t[x].sum;//這里是某道題的修改，據(jù)題目而定
else t[x].lda=t[x].rda=0,t[x].mx=y;
}void down(int x){
if(!x)return;
if(t[x].add!=maxn){
change(tt[x][0],t[x].add);
change(tt[x][1],t[x].add);
t[x].add=maxn;
}
}void remove(int x,int y){
do{
d[++d[0]]=x;
x=f[x];
}while(x!=y);
while(d[0])down(d[d[0]--]);
}這類東西支持區(qū)間修改的數(shù)據(jù)結(jié)構(gòu)都要用到的，但是splay中的有所不同，由于只有在旋轉(zhuǎn)的以后才用的到，例如splay(x,y)，所以需要把x到y(tǒng)的路徑上的標(biāo)記都下傳。
例如把x的子樹的區(qū)間翻轉(zhuǎn)。
void overturn(int x){
if(!x)return;
swap(tt[x][0],tt[x][1]);
t[x].biao^=1;
}其實很簡單，只需要把所有節(jié)點的左右兒子調(diào)換便可。注意懶標(biāo)記的biao要用^或1-biao，由于如果某段區(qū)間被同時翻轉(zhuǎn)兩次相當(dāng)于沒有翻轉(zhuǎn)。
int kth(int x,int k){
down(x);
if(t[tt[x][0]].size+1==k)return x;
if(t[tt[x][0]].size+1>k)return kth(tt[x][0],k);
else return kth(tt[x][1],k-t[tt[x][0]].size-1);
}這個很簡單啦。
其實如果想知道第x節(jié)點在序列中的序號的話，可以把x旋轉(zhuǎn)到根(及splay(x,0))，然后t[tt[x][0]].size+1就是x在原序列中的序號。
把x為根節(jié)點的這棵樹以原序列序號y為分水嶺，分成l和r兩顆子樹。
void split(int x,int y,int &l,int &r){
int j=kth(x,y);
splay(j,0);
l=j,r=t[j][1];
tt[l][1]=0;
f[r]=0;
update(j);
}把以x為根的樹和以y為根的樹合并為樹l。
為何要找到x樹中第 size[x]大(及在原序列中序號最大的節(jié)點)的節(jié)點，由于在原序列中序號最大的節(jié)點沒有右兒子，方便合并。
void merge(int x,int y,int &l){
int j=kth(x,size[x]);
splay(j,0);
tt[j][1]=y;
f[y]=j;
update(j);
l=j;
}比如說Link_Cut_Tree（及l(fā)ct或動態(tài)樹）……
目前也只知道這么多了，但是這些操作在大部份題目中都夠用了。
【CQOI2014】排序機(jī)械臂
【NOI2005】保護(hù)數(shù)列
甚么最大值，排序也能夠用splay來練練手。
程序員人生，我編程，我富裕，記住wfuyu網(wǎng)，php教程，php學(xué)習(xí)，php手冊，CMS模版制作
聲明：本站大部分內(nèi)容是作者原創(chuàng)，少部分收集于互聯(lián)網(wǎng)供大家一起學(xué)習(xí)，原版權(quán)很多不明，如有侵權(quán)請聯(lián)系本站，謝謝！
粵ICP備14040726號-1?? 2015-2020 程序員人生 版權(quán)所有
