本系列文章已全部上傳至我的github，地址：ZeeCoder‘s Github
歡迎大家關注我的新浪微博，我的新浪微博
歡迎轉載，轉載請注明出處
Given two words word1 and word2, find the minimum number of steps ?>required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
這道題1拿到就覺得需要用到動態計劃，因而斟酌到用遞歸來解決，3種情況，順次進行，可是隨著遞歸的加深，自但是然就超時了！
/*
注：此代碼沒有過量測試，如有毛病，請各位留言指出
*/
class Solution {
public:
int minDis = 1000000;
int minDistance(string word1, string word2) {
vector<int> minpath(10000,10000);
getMinDis(word1,word2,0,0,minpath);
return minDis;
}
void getMinDis(string word1, string word2, int idx, int count,vector<int>& minpath)
{
if(minpath[idx] <= count) return; //為了減少遞歸深度，可是還是超時了
if (word1 == word2) { minDis = minDis < count ? minDis : count; return; }
//如果該位上相等則繼續
if(idx < word1.size() && idx < word2.size() && word1[idx] == word2[idx]) getMinDis(word1, word2, idx + 1, count,minpath);
else {
if (idx < word1.size())//idx小于word1的時候才能刪除
{
string tword1 = word1;
tword1.erase(tword1.begin() + idx);
getMinDis(tword1, word2, idx, count + 1,minpath);
}
if (idx < word2.size()) //插入話需要idx小于Word2的長度
{
string tword1 = word1;
tword1.insert(idx, 1, word2[idx]);
getMinDis(tword1, word2, idx + 1, count + 1,minpath);
}
if (idx < word1.size() && idx < word2.size())//替換則需要都小于
{
string tword1 = word1;
tword1[idx] = word2[idx];
getMinDis(tword1, word2, idx + 1, count + 1,minpath);
}
}
}
};下面，主角出現了！看到這個算法真正覺得算法的美好了，由繁化簡！
首先我們定義1個數組，dp[i][j]，這個數組代表了word1的0~i轉換到word2的0~j需要的最小步數。很明顯，該矩陣應當初始化為：dp[0][i] = i和dp[i][0] = i，以下圖（以ACE->ADEF為例）：
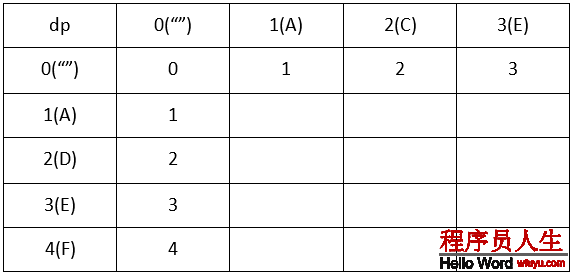
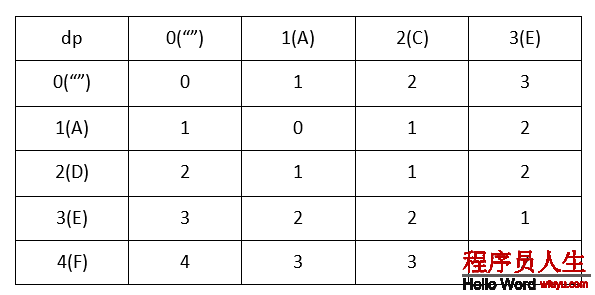
class Solution {
public:
int minDistance(string word1, string word2) {
int row = word1.length();
int col = word2.length();
//初始化
vector<vector<int>> dpath(row+1,vector<int>(col+1,0));
for(int i = 0 ; i < col+1 ; i++)/
{
dpath[0][i] = i;
}
for(int i = 0 ; i < row+1 ;i++)
{
dpath[i][0] = i;
}
for(int i = 1; i < row+1 ;i++)
{
for(int j = 1 ; j < col+1;j++)
{
//3者取最小
dpath[i][j] = min(dpath[i-1][j]+1,dpath[i][j-1]+1);
dpath[i][j] = min(dpath[i][j],dpath[i-1][j-1]+(word1[i-1] == word2[j-1]?0:1));
}
}
return dpath[row][col];
}
};
上一篇 Git學習筆記整理
程序員人生，我編程，我富裕，記住wfuyu網，php教程，php學習，php手冊，CMS模版制作
聲明：本站大部分內容是作者原創，少部分收集于互聯網供大家一起學習，原版權很多不明，如有侵權請聯系本站，謝謝！
粵ICP備14040726號-1?? 2015-2020 程序員人生 版權所有
