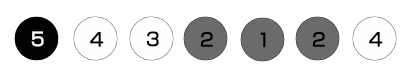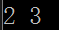圖的深度優先搜索及拓撲排序
來源:程序員人生 發布時間:2016-06-21 08:00:50 閱讀次數:3826次
本文將介紹圖的深度優先搜索,并實現基于深度優先搜索的拓撲排序(拓撲排序適用于有向無環圖,下面詳細介紹)。
1. 圖的深度優先遍歷要解決的問題
圖的深度優先搜索與樹的深度優先搜索類似,但是對圖進行深度優先搜索要解決1個問題,那就是頂點的重復訪問,假定圖中存在1個環路A-B-C-A,那末對頂點A進行展開后得到B,對B進行展開后得到C,然后對C進行展開后得到A,然后A就被重復訪問了。。。
這明顯是不對的!我們需要用1個狀態變量來記錄1個頂點被訪問和被展開的狀態。在《算法導論》中,作者使用3種色彩來對此進行標記:WHITE——頂點還沒被訪問過,GRAY——頂點已被訪問過但是其子結點還沒被訪問完,BLACK——頂點已被訪問過而且其子結點已被訪問完了。
2. 用棧實現圖的深度優先遍歷
在《算法導論》中,作者使用了遞歸來實現深度優先遍歷。雖然遞歸寫起來更加簡潔而且容易理解,但是我其實不建議在實際工程中這樣做,除非你的問題范圍比較小。否則遞歸會讓你的程序萬劫不復。正如使用隊列實現廣度優先搜索1樣(可以看到我的上1篇博客圖的廣度優先遍歷),下面我將會使用棧來實現深度優先搜索。
下面用1個例子來講明如何使用棧來實現深度優先遍歷。假定有下面1個圖。
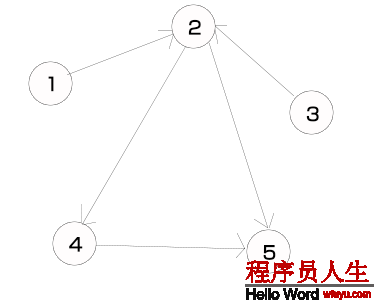
首先,我們初始化1個空棧,然后將所有頂點入棧,此時所有頂點都沒有被訪問過,因此所有頂點都置為白色,以下所示。
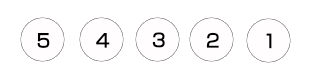
上述初始化完成以后,頂點5位于棧底,頂點1位于棧頂,然后我們就進入循環操作,首先出棧1個頂點,該頂點為頂點1,由于頂點1是白色的,即沒有被訪問過,因而就將頂點1置為灰色,并重新入棧(由于下面要記錄結點的子結點被訪問完的次序),然后展開頂點1的所有頂點,只有頂點2,由于頂點2是白色即未被訪問過,因而將頂點2入棧,以下圖所示。
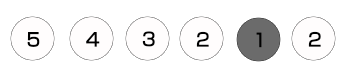
然后我們繼續循環,出棧1個頂點,即頂點2,由于頂點2是白色的,因而將其置為灰色,并重新入棧,然后展開得到頂點4和頂點5,由于頂點4和頂點5均為白色,因而將它們都入棧。以下圖所示。

然后還是繼續循環,出棧1個頂點,即頂點5,由于頂點5是白色的,因而將其置為灰色,并重新入棧,然后展開頂點5,發現頂點5沒有子結點,以下圖所示。

然后繼續循環,出棧頂點5,此時頂點5為灰色,說明頂點5的子結點已被訪問完了,因而將頂點5置為黑色,并將其次序標記為1,說明他是第1個被展開完的結點,這1個記錄將會被利用到拓撲排序中。此時棧的狀態以下所示。
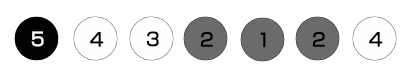
繼續循環,出棧頂點4,由于是白色的,所以將頂點4置為灰色并重新入棧,然后展開頂點4得到頂點5,由于頂點5是黑色的,因而不將其入棧。接下來繼續出棧頂點4,發現頂點4是灰色的,因而和前面1樣,將頂點4置為黑色并將其次序記錄為2。此時的棧以下圖所示。

好了,后面的循環的工作也跟上述類似,順次將頂點2、1出棧并置為黑色,直到頂點3展開發現沒有白色的子結點,也將其置為黑色。然后再到了頂點4和頂點5,由于是黑色,直接出棧不作任何處理了。此時棧為空,遍歷結束。
我們的程序需要的輸入的圖以鄰接表的情勢表示,下面給出圖及頂點和鄰接表的定義。
typedef enum VertexColor
{
Vertex_WHITE = 0, // 未被搜索到
Vertex_BLACK = 1, // 子結點都被搜索終了
Vertex_GRAY = 2 // 子結點正在被搜索
} VertexColor;
typedef struct GNode
{
int number; // 頂點編號
struct GNode *next;
} GNode;
typedef struct Vertex
{
int number;
int f;
VertexColor color; // 搜索進程標記搜索狀態
struct Vertex *p;
} Vertex;
typedef struct Graph
{
GNode *LinkTable;
Vertex *vertex;
int VertexNum;
} Graph;
VertexColor是頂點的色彩枚舉量定義。GNode是鄰接表的元素定義,其記錄了頂點的編號。鄰接表本質上就是1個指針數組,其每一個元素都是指向1個鏈表的第1個元素的指針。Vertex是頂點的數據結構,其屬性number為頂點編號,f是記錄其被訪問完的次序,color是狀態標識色彩,p指向搜索完成后得到的深度優先遍歷樹中的頂點的先驅。Graph是圖的數據結構定義,其包括了1個頂點數組,按編號升序排列,LinkTable是鄰接表。
下面給出用棧實現的深度優先搜索的程序。
/**
* 深度優先搜索,要求輸入圖g的結點編號從1開始
*/
void searchByDepthFirst(Graph *g)
{
int VertexNum = g->VertexNum;
Stack *stack = initStack();
Vertex *vs = g->vertex;
GNode *linkTable = g->LinkTable;
int order = 0;
for (int i = 0; i < VertexNum; i++)
{
Vertex *v = vs + i;
v->color = Vertex_WHITE;
v->p = NULL;
push(&stack, v->number);
}
while (!isEmpty(stack))
{
int number = pop(&stack);
Vertex *u = vs + number - 1;
if (u->color == Vertex_WHITE)
{
// 開始搜索該結點的子結點
u->color = Vertex_GRAY;
push(&stack, number);
}
else if (u->color == Vertex_GRAY)
{
// 該結點的子結點已被搜索完了
u->color = Vertex_BLACK;
u->f = order++;
continue;
}
else
{
continue;
}
GNode *links = linkTable + number - 1;
links = links->next;
while (links != NULL)
{
// 展開子結點并入棧
Vertex *v = vs + links->number - 1;
if (v->color == Vertex_WHITE)
{
v->p = u;
push(&stack, links->number);
}
links = links->next;
}
}
}
程序先將所有頂點初始化為白色并入棧,然后開始循環。在循環中,每次出棧1個結點都要先對其色彩進行判斷,如果是灰色,標記其被訪問完成的次序并標為黑色,如果是黑色,不作任何處理,如果是白色,則置為灰色并重新入棧,然后展開其所有子結點并將白色的子結點入棧,并且記下這些白色頂點的先驅。當棧為空時,循環結束。
棧的操作可以參考其它資料,這里不做詳述,下面給出1個簡單實現。
typedef struct Stack {
int value;
struct Stack *pre;
} Stack;
上面是棧的結構定義。
Stack* initStack()
{
Stack *s = (Stack *)malloc(sizeof(Stack));
s->pre = NULL;
return s;
}
void push(Stack **s, int value)
{
Stack *n = (Stack *)malloc(sizeof(Stack));
n->pre = *s;
n->value = value;
*s = n;
}
int pop(Stack **s)
{
if ((*s)->pre == NULL)
{
return INT_MAX;
}
int value = (*s)->value;
Stack *pre = (*s)->pre;
free(*s);
*s = pre;
return value;
}
int isEmpty(Stack *s)
{
if (s->pre == NULL)
{
return 1;
}
return 0;
}
void destroyStack(Stack **s)
{
while (*s != NULL)
{
Stack *pre = (*s)->pre;
free(*s);
*s = pre;
}
}
上面是棧的方法,順次是初始化1個空棧,入棧,出棧,判斷是不是為空棧,燒毀棧。
下面給出1個利用上述深度優先遍歷方法的例子代碼和運行結果。
Graph graph;
graph.VertexNum = 5;
Vertex v[5];
Vertex v1; v1.number = 1; v1.p = NULL; v[0] = v1;
Vertex v2; v2.number = 2; v2.p = NULL; v[1] = v2;
Vertex v3; v3.number = 3; v3.p = NULL; v[2] = v3;
Vertex v4; v4.number = 4; v4.p = NULL; v[3] = v4;
Vertex v5; v5.number = 5; v5.p = NULL; v[4] = v5;
graph.vertex = v;
GNode nodes[5];
GNode n1; n1.number = 1;
GNode n2; n2.number = 2;
GNode n3; n3.number = 3;
GNode n4; n4.number = 4;
GNode n5; n5.number = 5;
GNode y; y.number = 5;
GNode e; e.number = 2;
GNode f; f.number = 5;
GNode g; g.number = 2;
GNode h; h.number = 4;
n1.next = &e; e.next = NULL;
n2.next = &h; h.next = &f; f.next = NULL;
n3.next = &g; g.next = NULL;
n4.next = &y; y.next = NULL;
n5.next = NULL;
nodes[0] = n1;
nodes[1] = n2;
nodes[2] = n3;
nodes[3] = n4;
nodes[4] = n5;
graph.LinkTable = nodes;
searchByDepthFirst(&graph);
printf("\n");
printPath(&graph, 2);
運行結果以下。
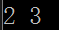
上述示例代碼對本文前面給出的圖進行深度優先遍歷后,輸出頂點2的先驅子樹,得到上述結果,意思是頂點2的先驅頂點為3。
3. 圖的拓撲排序
圖的拓撲排序可以利用深度優先遍歷來實現。
首先,說明1下甚么是拓撲排序。拓撲排序是指將圖按前后順序組織排列起來,前后順序是指在排序結果中,前面的頂點多是有1條簡單路徑通向后面的頂點的,而后面的頂點是肯定沒有1條簡單路徑通向前面的頂點的。拓撲排序適用于有向無環圖。下面給出1個拓撲排序的例子。

還是這個圖,這也是1個有向無環圖,拓撲排序的結果最前面的頂點肯定是1個根頂點,即沒有其它頂點指向他。這個圖的拓撲排序結果是1、3、2、4、5,或1、3、2、5、4,等等,不存在指向關系的頂點間的順序是不肯定的。我們可以將拓撲排序的圖看成是1個日程表,頂點1代表洗臉,頂點3代表刷牙,頂點2代表吃早飯,頂點4代表穿褲子,頂點5代表穿衣服,因而拓撲排序本質就是根據事件應當產生的前后順序組織起來。
圖的深度優先遍歷有1個特點,那就是,當1個頂點的子結點都被訪問完了,該頂點才會結束訪問,并開始向上回溯訪問它的父結點的其它子結點。這意味著,1個頂點的結束訪問時間與其子結點的結束訪問時間存在前后關系,而這個順序恰好與拓撲排序是相反的!簡單地說,在深度優先遍歷中,頂點A要結束訪問的條件是其子結點B、C、D...都被訪問完了,而在拓撲排序中,事件A完成以后其后面的事件B、C、D...才可以繼續進行。這也就是上面的深度優先搜索為何要記錄結點被訪問完成的次序,由于這個次序倒過來就是拓撲排序的順序!
下面給出基于圖的深度優先搜索實現的拓撲排序的程序。
/**
* 有向無環圖的拓撲排序
*/
void topologySort(Graph *g, int **order, int *n)
{
searchByDepthFirst(g);
*n = g->VertexNum;
*order = (int *)malloc(sizeof(int) * *n);
for (int i = 0; i < *n; i++)
{
(*order)[*n - 1 - g->vertex[i].f] = i + 1;
}
}
一樣的,上述程序實現的拓撲排序要求的圖的頂點編號也是從1開始。
其實拓撲排序還有另外一種實現方法,那就是從根頂點開始,刪除所有根頂點及與之相連的邊。此時就會產生新的根頂點,然后繼續重復上述操作,知道所有頂點都被刪除。
4. 總結
本文介紹了如何使用棧來實現圖的深度優先搜索,并基于圖的深度優先搜索實現了拓撲排序。其時間復雜度均為O(n)。完全程序可以參考我的github項目數據結構與算法
這個項目里面有本博客介紹過的和沒有介紹的和將要介紹的《算法導論》中部份主要的數據結構和算法的C實現,有興趣的可以fork或star1下哦~ 由于本人還在研究《算法導論》,所以這個項目還會延續更新哦~ 大家1起好好學習~
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈


![]()
![]()
![]()
![]()