數據結構例程――二叉樹的構造
來源:程序員人生 發布時間:2016-05-12 10:07:17 閱讀次數:2462次
本文是數據結構基礎系列(6):樹和2叉樹中第13課時2叉樹的構造的例程。
1.由先序序列和中序序列構造2叉樹
-
定理:任何n(n≥0)個不同節點的2叉樹,都可由它的中序序列和先序序列唯1地肯定。
-
證明(數學歸納法)
基礎:當n=0時,2叉樹為空,結論正確。
假定:設節點數小于n的任何2叉樹,都可以由其先序序列和中序序列唯1地肯定。
歸納:已知某棵2叉樹具有n(n>0)個不同節點,其先序序列是a0a1…an?1;中序序列是b0b1…bk?1bkbk+1…bn?1。
-
先序遍歷“根-左-右”,a0一定是2叉樹的根節點
-
a0必定在中序序列中出現,設在中序序列中必有某個bk(0≤k≤n?1)就是根節點a0。

-
由于bk是根節點,中序遍歷“左-根-右”,故中序序列中b0b1…bk?1必是根節點bk(a0)左子樹的中序序列,即bk的左子樹有k個節點,bk+1…bn?1必是根節點bk(a0)右子樹的中序序列,即bk的右子樹有n?k?1個節點。
-
對應先序序列,緊跟在根節點a0以后的k個節點a1…ak是左子樹的先序序列,ak+1…an?1這n?k?1就是右子樹的先序序列。

-
根據歸納假定,子先序序列a1…ak和子中序序列b0b1…bk?1可以唯1地肯定根節點a0的左子樹,而先序序列ak+1…an?1和子中序序列bk+1…bn?1可以唯1地肯定根節點a0的右子樹。
-
綜上所述,這棵2叉樹的根節點己經肯定,而且其左、右子樹都唯1地肯定了,所以全部2叉樹也就唯1地肯定了。
-
例
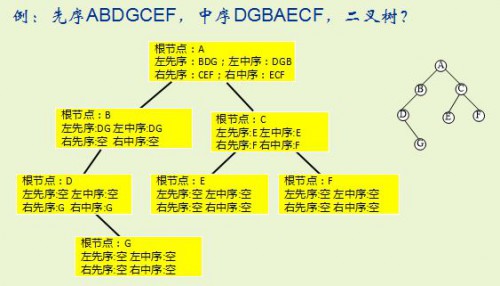
根據定理的證明,寫出下面的算法。
品味:以上構造性證明是突出體現計算機科學的案例。計算機學科的精華就在于制造,即便在“理論性”味道的定理中,其證明進程,給出的就是“存在的這么1個東西”的構造方法。
[參考解答](btreee.h見算法庫)
#include #include #include "btree.h" BTNode *CreateBT1(char *pre,char *in,int n) {
BTNode *s; char *p; int k; if (n<=0) return NULL;
s=(BTNode *)malloc(sizeof(BTNode)); s->data=*pre; for (p=in; p<in+n; p++) if (*p==*pre) break; k=p-in; s->lchild=CreateBT1(pre+1,in,k); s->rchild=CreateBT1(pre+k+1,p+1,n-k-1); return s;
} int main()
{
ElemType pre[]="ABDGCEF",in[]="DGBAECF";
BTNode *b1;
b1=CreateBT1(pre,in,7);
printf("b1:");
DispBTNode(b1);
printf("
"); return 0;
}
2.由后序序列和中序序列構造2叉樹
-
定理:任何n(n>0)個不同節點的2叉樹,都可由它的中序序列和后序序列唯1地肯定。
-
證明:(略)

[參考解答](btreee.h見算法庫)
#include #include #include "btree.h" BTNode *CreateBT2(char *post,char *in,int n) {
BTNode *s; char r,*p; int k; if (n<=0) return NULL;
r=*(post+n-1); s=(BTNode *)malloc(sizeof(BTNode)); s->data=r; for (p=in; p<in+n; p++) if (*p==r) break;
k=p-in; s->lchild=CreateBT2(post,in,k); s->rchild=CreateBT2(post+k,p+1,n-k-1); return s;
} int main()
{
ElemType in[]="DGBAECF",post[]="GDBEFCA";
BTNode *b2;
b2=CreateBT2(post,in,7);
printf("b2:");
DispBTNode(b2);
printf("
"); return 0;
}
3.由順序存儲結構轉為2叉鏈存儲結構
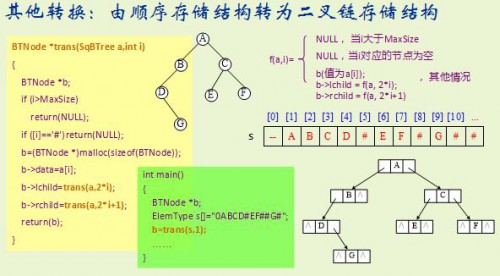
[參考解答](btreee.h見算法庫)
#include #include #include "btree.h" #define N 30 typedef ElemType SqBTree[N];
BTNode *trans(SqBTree a,int i)
{
BTNode *b; if (i>N) return(NULL); if (a[i]==#) return(NULL); b=(BTNode *)malloc(sizeof(BTNode)); b->data=a[i];
b->lchild=trans(a,2*i); b->rchild=trans(a,2*i+1); return(b); } int main()
{
BTNode *b;
ElemType s[]="0ABCD#EF#G####################";
b=trans(s,1); printf("b:");
DispBTNode(b); printf("
"); return 0;
}
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈






