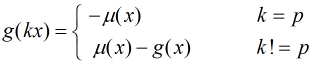莫比烏斯反演
來源:程序員人生 發布時間:2015-08-20 08:26:09 閱讀次數:4296次
莫比烏斯反演在數論中占有重要的地位,許多情況下能大大簡化運算。那末我們先來認識莫比烏斯反演公式。
定理: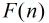 和
和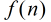 是定義在非負整數集合上的兩個函數,并且滿足條件
是定義在非負整數集合上的兩個函數,并且滿足條件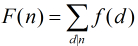 ,那末我們得到結論
,那末我們得到結論
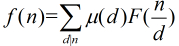
在上面的公式中有1個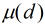 函數,它的定義以下:
函數,它的定義以下:
(1)若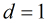 ,那末
,那末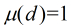
(2)若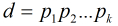 ,
,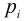 均為互異素數,那末
均為互異素數,那末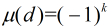
(3)其它情況下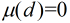
對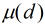 函數,它有以下的常見性質:
函數,它有以下的常見性質:
(1)對任意正整數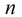 有
有
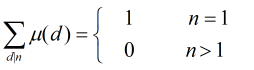
(2)對任意正整數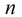 有
有
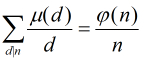
線性挑選求莫比烏斯反演函數代碼。
void Init()
{
memset(vis,0,sizeof(vis));
mu[1] = 1;
cnt = 0;
for(int i=2; i<N; i++)
{
if(!vis[i])
{
prime[cnt++] = i;
mu[i] = ⑴;
}
for(int j=0; j<cnt&&i*prime[j]<N; j++)
{
vis[i*prime[j]] = 1;
if(i%prime[j]) mu[i*prime[j]] = -mu[i];
else
{
mu[i*prime[j]] = 0;
break;
}
}
}
}
有了上面的知識,現在我們來證明莫比烏斯反演定理。
證明
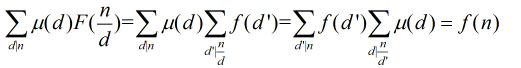
證明終了!
嗯,有了莫比烏斯反演,很多問題都可以簡化了,接下來我們來看看莫比烏斯反演在數論中如何簡化運算的。
題目:http://bz.cdqzoi.com/JudgeOnline/problem.php?id=2818
題意:給1個正整數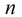 ,其中
,其中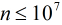 ,求使得
,求使得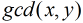 為質數的
為質數的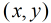 的個數,
的個數,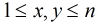 。
。
分析:對本題,由于是使得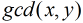 為質數,所以必定要枚舉小于等于
為質數,所以必定要枚舉小于等于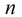 的質數,那末對每個質數
的質數,那末對每個質數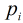 ,只
,只
需要求在區間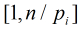 中,滿足有序對
中,滿足有序對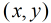 互質的對數。
互質的對數。
也就是說,現在問題轉化為:在區間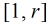 中,存在多少個有序對使得
中,存在多少個有序對使得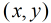 互質,這個問題就簡單啦,由于
互質,這個問題就簡單啦,由于
是有序對,無妨設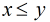 ,那末我們如果枚舉每個
,那末我們如果枚舉每個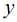 ,小于
,小于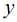 有多少個
有多少個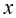 與
與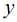 互素,這正是歐拉函數。所以
互素,這正是歐拉函數。所以
我們可以遞推法求歐拉函數,將得到的答案乘以2便可,但是這里乘以2后還有漏計算了的,那末有哪些呢?
是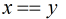 且為素數的情況,再加上就好了。
且為素數的情況,再加上就好了。
代碼:
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <bitset>
using namespace std;
typedef long long LL;
const int N = 10000010;
bitset<N> prime;
LL phi[N];
LL f[N];
int p[N];
int k;
void isprime()
{
k = 0;
prime.set();
for(int i=2; i<N; i++)
{
if(prime[i])
{
p[k++] = i;
for(int j=i+i; j<N; j+=i)
prime[j] = false;
}
}
}
void Init()
{
for(int i=1; i<N; i++) phi[i] = i;
for(int i=2; i<N; i+=2) phi[i] >>= 1;
for(int i=3; i<N; i+=2)
{
if(phi[i] == i)
{
for(int j=i; j<N; j+=i)
phi[j] = phi[j] - phi[j] / i;
}
}
f[1] = 0;
for(int i=2;i<N;i++)
f[i] = f[i⑴] + (phi[i]<<1);
}
LL Solve(int n)
{
LL ans = 0;
for(int i=0; i<k&&p[i]<=n; i++)
ans += 1 + f[n/p[i]];
return ans;
}
int main()
{
Init();
isprime();
int n;
scanf("%d",&n);
printf("%I64d
",Solve(n));
return 0;
}
嗯,上題不算太難,普通的歐拉函數就能夠弄定,接下來我們來看看它的升級版。
題意:給定兩個數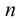 和
和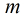 ,其中
,其中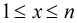 ,
,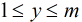 ,求
,求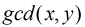 為質數的
為質數的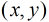 有多少對?其中
有多少對?其中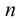 和
和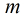 的范
的范
圍是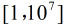 。
。
分析:本題與上題不同的是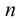 和
和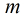 不1定相同。在這里我們用莫比烏斯反演來解決,文章開頭也說了它能大大簡化
不1定相同。在這里我們用莫比烏斯反演來解決,文章開頭也說了它能大大簡化
運算。我們知道莫比烏斯反演的1般描寫為:
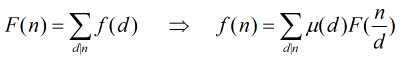
其實它還有另外一種描寫,本題也是用到這類。那就是:
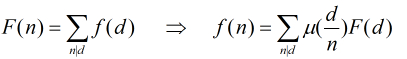
好了,到了這里,我們開始進入正題。。。
對本題,我們設
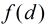 為滿足
為滿足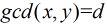 且
且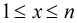 和
和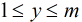 的
的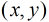 的對數
的對數
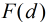 為滿足
為滿足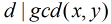 且
且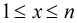 和
和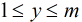 的
的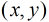 的對數
的對數
那末,很明顯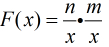 ,反演后得到
,反演后得到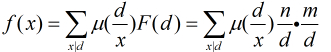
由于題目要求是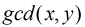 為質數,那末我們枚舉每個質數
為質數,那末我們枚舉每個質數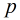 ,然后得到
,然后得到
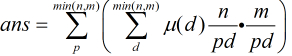
如果直接這樣做肯定TLE,那末我們必須優化。
我們設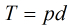 ,那末繼續得到
,那末繼續得到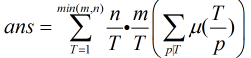 。
。
到了這里,可以看出如果我們可以先預處理出所有的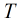 對應的
對應的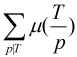 的值,那末本題就解決了。
的值,那末本題就解決了。
我們設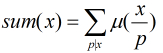 ,注意這里
,注意這里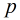 為素數,
為素數,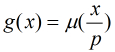 。
。
那末,我們枚舉每個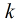 ,得到
,得到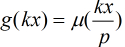 ,現在分情況討論:
,現在分情況討論:
(1)如果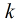 整除
整除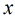 ,那末得到
,那末得到
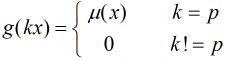
(2)如果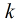 不整除
不整除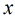 ,那末得到
,那末得到
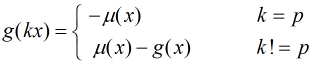
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N = 10000005;
bool vis[N];
int p[N];
int cnt;
int g[N],u[N],sum[N];
void Init()
{
memset(vis,0,sizeof(vis));
u[1] = 1;
cnt = 0;
for(int i=2;i<N;i++)
{
if(!vis[i])
{
p[cnt++] = i;
u[i] = ⑴;
g[i] = 1;
}
for(int j=0;j<cnt&&i*p[j]<N;j++)
{
vis[i*p[j]] = 1;
if(i%p[j])
{
u[i*p[j]] = -u[i];
g[i*p[j]] = u[i] - g[i];
}
else
{
u[i*p[j]] = 0;
g[i*p[j]] = u[i];
break;
}
}
}
sum[0] = 0;
for(int i=1;i<N;i++)
sum[i] = sum[i⑴] + g[i];
}
int main()
{
Init();
int T;
scanf("%d",&T);
while(T--)
{
LL n,m;
cin>>n>>m;
if(n > m) swap(n,m);
LL ans = 0;
for(int i=1,last;i<=n;i=last+1)
{
last = min(n/(n/i),m/(m/i));
ans += (n/i)*(m/i)*(sum[last]-sum[i⑴]);
}
cout<<ans<<endl;
}
return 0;
}
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈

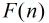 和
和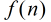 是定義在非負整數集合上的兩個函數,并且滿足條件
是定義在非負整數集合上的兩個函數,并且滿足條件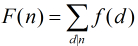 ,那末我們得到結論
,那末我們得到結論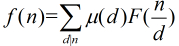
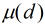 函數,它的定義以下:
函數,它的定義以下: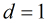 ,那末
,那末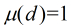
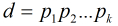 ,
,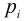 均為互異素數,那末
均為互異素數,那末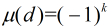
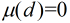
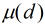 函數,它有以下的常見性質:
函數,它有以下的常見性質: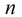 有
有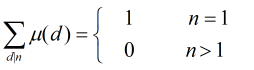
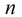 有
有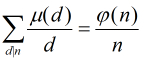
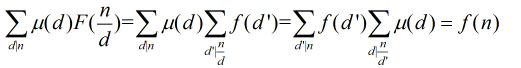
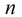 ,其中
,其中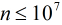 ,求使得
,求使得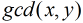 為質數的
為質數的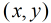 的個數,
的個數,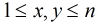 。
。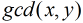 為質數,所以必定要枚舉小于等于
為質數,所以必定要枚舉小于等于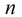 的質數,那末對每個質數
的質數,那末對每個質數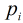 ,只
,只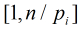 中,滿足有序對
中,滿足有序對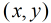 互質的對數。
互質的對數。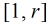 中,存在多少個有序對使得
中,存在多少個有序對使得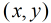 互質,這個問題就簡單啦,由于
互質,這個問題就簡單啦,由于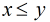 ,那末我們如果枚舉每個
,那末我們如果枚舉每個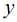 ,小于
,小于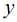 有多少個
有多少個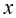 與
與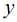 互素,這正是歐拉函數。所以
互素,這正是歐拉函數。所以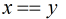 且為素數的情況,再加上就好了。
且為素數的情況,再加上就好了。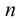 和
和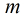 ,其中
,其中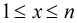 ,
,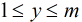 ,求
,求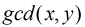 為質數的
為質數的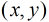 有多少對?其中
有多少對?其中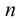 和
和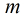 的范
的范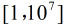 。
。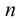 和
和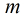 不1定相同。在這里我們用莫比烏斯反演來解決,文章開頭也說了它能大大簡化
不1定相同。在這里我們用莫比烏斯反演來解決,文章開頭也說了它能大大簡化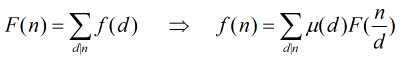
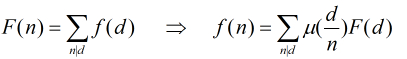
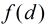 為滿足
為滿足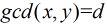 且
且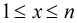 和
和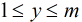 的
的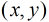 的對數
的對數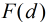 為滿足
為滿足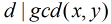 且
且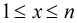 和
和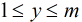 的
的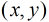 的對數
的對數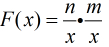 ,反演后得到
,反演后得到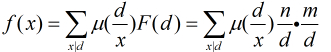
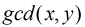 為質數,那末我們枚舉每個質數
為質數,那末我們枚舉每個質數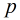 ,然后得到
,然后得到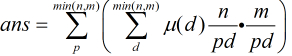
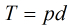 ,那末繼續得到
,那末繼續得到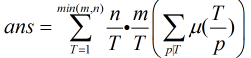 。
。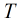 對應的
對應的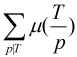 的值,那末本題就解決了。
的值,那末本題就解決了。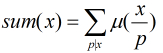 ,注意這里
,注意這里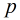 為素數,
為素數,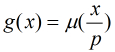 。
。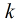 ,得到
,得到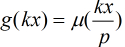 ,現在分情況討論:
,現在分情況討論: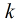 整除
整除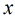 ,那末得到
,那末得到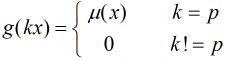
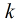 不整除
不整除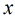 ,那末得到
,那末得到