貪心算法就是做出1系列選擇來使原問題到達最優解。在每個決策點,都是做出當前看來的最優選擇,比如在活動選擇問題里面,我們總是在1個問題的基礎上選擇結束時間最早的活動,以后再在剩下活動的基礎上選出結束時間最早的活動,以此類推,直到沒有活動可以進行選擇。但是遺憾的是這類算法其實不是總能得到最優解,并且是不是能得到最優解還取決于對貪心策略的選擇。
1般來講,設計貪心算法觸及到下面幾個步驟:
1.肯定問題的最優子結構
2.基于問題的最優子結構設計1個遞歸算法
3.證明我們做出的貪心選擇,只剩下1個子問題
4.證明貪心選擇總是安全的
5.設計1個遞歸算法實現貪心策略
6.將貪心算法轉化為迭代算法
比如在活動選擇問題里面,我們就是肯定了互動最優子結構的性質,我們在子問題
更1般的來講,我們可以講貪心算法的設計步驟簡述為下面幾部:
1.將最優化問題簡化為這樣的情勢:最初1個選擇以后,只剩下1個子問題需要求解!
2.證明在做出貪心選擇以后,原問題總是存在最優解,即貪心選擇總是安全的!
3.證明在做出貪心選擇以后,剩下的子問題滿足性質:其最優解與做出選擇的組合在1起得到原問題的最優解,即最優子結構
貪心算法有兩個重要的性質:
- 貪心選擇性質
- 最優子結構性質
下面我們來詳細討論這兩個性質
第1個關鍵要素就是貪心選擇性質:我們可以做出局部最優選擇來構造最優解。也就是說,我們在做出選擇時,總是以當前的情況為基礎做出最優選擇的,而不用斟酌子問題的解!
這要是和動態計劃最大的不同的地方,我們知道
- 在動態計劃中,在每次做出1個選擇的時候總是要將所有選擇進行比較以后才能肯定到底采取哪種選擇,而這類選擇的參考根據是以子問題的解為基礎的,所以動態計劃總是采取自下而下的方法來,先得到子問題的解,再通過子問題的解構造原問題的解。就算是自上而下的算法也是先求出子問題的解,通過遞歸調用自下而上的返回每個子問題的最優解
- 在貪心算法中,我們總是在原問題的基礎上做出1個選擇,然后求解剩下的唯1子問題,貪心算法歷來都不依賴子問題的解,不過有可能會依賴上1次做出的選擇,所以貪心算法是自上而下的。1步1步的選擇將原問題1步步消減得更小
固然,我們必須證明每個步驟做出的貪心選擇都可以生玉成局最優解!我們再活動選擇問題里面是這樣的做的,首先假定有1個最優解,然后將做出的選擇替換進去得到另外1個最優解!
如果1個問題的最優解包括其子問題的最優解,那末就稱這個問題具有最優子結構性質!我們知道最優子結構這個性質是動態計劃和貪心算法都必須具有的關鍵性質。
貪心算法和動態計劃都有1些共同的性質,比如最優子結構,有些問題我們可以采取動態計劃來解決,也能夠采取貪心算法來結局,這二者之間有細微的差別!下面我們通過研究1個問題來辨別之間的差別!
下面有兩個經典的算法問題:
0⑴背包問題:我們有1堆物品
S={a1,a2,...,an} ,每個物品ai 都有1個重量wi 和1個價值vi .現在有1個背包,這個背包的容量為W ,現在要將這些物品在不超越背包容量的情況下選擇性的放入背包,使得背包里面物品的價值最大,物品不能只選取其中1部份,必須選擇全部,或不選!分數背包問題:這個問題和上面的問題比較類似,唯1不同的就是該問題里面的物品可以進行分割,便可以只選取1個物品
ai 的1部份
雖然上面兩個問題比較類似,但是貪心算法可以求解第2個問題而不能求解0⑴背包問題,為了求解分數背包問題,我們首先得到每個物品單位重量的價值
下面我們來證明1下上面貪心選擇的料想:
證明:
我們首先假定我們有1個最優解
A1 ,那末我們首先找到A1 里面平均價值最高的物品am ,讓后我們將用商品里面平均價值最高的物品a1 將am 進行全部替換或部份替換得到解A2 ,又因v1/w1≥vm/wm 所以A2 的總價值高于A1 的總價值,這A1 是最優解矛盾,因而得到A1 里面包括平均價值最高的物品。
因而我們得到最優子結構
為了說明這個貪心策略對0⑴背包問題無效,我們采取下面的例子
我們有3個物品和1個容量為50的背包,這3個物品<重量,價值>分別為:
a1<10,60>,a2<20,100>,a3<30,120> .
如果依照上面的貪心策略來選擇的話,首先是選擇
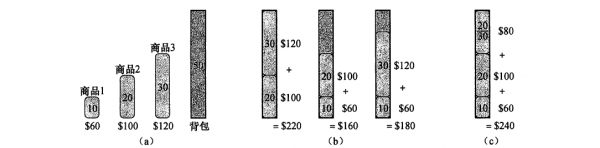
所以上面的貪心選擇將不能解決0⑴背包問題,但是卻可以完善的解決分數背包問題,那末0⑴背包問題要怎樣解決,由于這兩個背包問題都有1個很重要的性質,那就是最優子結構,因而乎動態計劃這個利器就要出手啦!
我們將在另外1篇文章里面介紹0⑴背包問題和分數背包問題!
文章中難免有疏漏,望批評指正!
