先來介紹幾個與歐拉函數有關的定理:
定理1:設m與n是互素的正整數,那末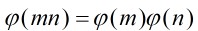
定理2:當n為奇數時,有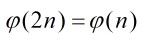 。
。
由于2n是偶數,偶數與偶數1定不互素,所以只斟酌2n與小于它的奇數互素的情況,則恰好就等于n的歐拉函數值。
定理3:設p是素數,a是1個正整數,那末
關于這個定理的證明用到容斥:
由于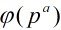 表示小于
表示小于 與
與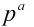 互素數的正整數個數,所以用
互素數的正整數個數,所以用 減去與它不互素的數的個數就好了。
減去與它不互素的數的個數就好了。
那末小于 與
與 不互素數的個數就是p的倍數個數,有
不互素數的個數就是p的倍數個數,有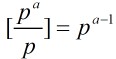 個。所以定理得證。
個。所以定理得證。
定理4:設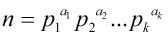 為正整數n的素數冪分解,那末
為正整數n的素數冪分解,那末
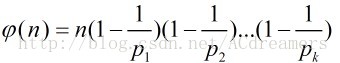
這個定理可以根據定理1和定理3證明,其實用到的就是容斥。如果對容斥熟習,其實完全就能夠直接容斥。
定理5:設n是1個正整數,那末
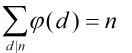
這個其實可以看莫比烏斯反演就明白了。
定理6:設m是正整數,(a,m)=1,則: 是同于方程
是同于方程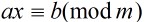 的解。
的解。
定理7:如果n大于2,那末n的歐拉函數值是偶數。
求歐拉函數值:
利用遞推法求歐拉函數值:
算法原理:開始令i的歐拉函數值等于它本身,如果i為偶數,可以利用定理2變成求奇數的。
若p是1個正整數滿足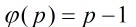 ,那末p是素數,在遍歷進程中如果遇到歐拉函數值等于本身的情況,那末
,那末p是素數,在遍歷進程中如果遇到歐拉函數值等于本身的情況,那末
說明該數為素數。把這個數的歐拉函數值改變,同時也把能被該素因子整除的數改變。
