線段樹
來源:程序員人生 發布時間:2015-06-17 09:08:45 閱讀次數:3671次
線段樹簡介:
線段樹的定義以下:
1棵2叉樹,記為T (a,b),參數a,b表示該結點表示區間[a,b]。區間的長度b-a記為L。遞歸定義T[a,b]:
若L>1 :[a, (a+b) div 2]為 T的左兒子
[(a+b)div 2,b]為T的右兒子。
若L=1 :T為1個葉子結點。
表示區間[1, 10]的線段樹表示以下:
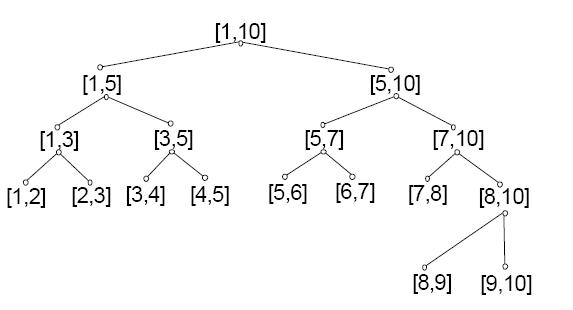
樹1般有兩種情勢:1、以點為結點。2、以線段為結點。區分如圖:上面1個以線段為結點,下面1個以點為結點:
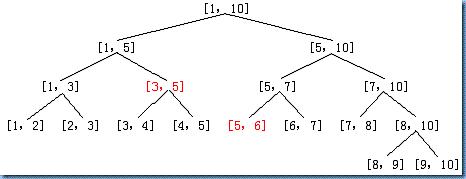
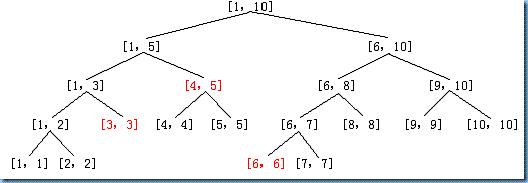
對線段樹存在:
定理:線段樹把區間上的任意1條線段都分成不超過2logL條線段。
這個結論為線段樹能在O(logL)的時間內完成1條線段的插入、刪除、查找等工作,提供了理論根據。
對線段樹的可以進行擴大。
1. 測度。結點所表示區間中線段覆蓋過的長度,存儲在各結點中。
2. 獨立線段數。區間中互不相交的線段條數。
3. 權和。區間所有元線段的權和。
測度的遞推公式以下:
a[j] - a[i] 該結點 Count>0
M = 0 該結點為葉結點且 Count=0
Leftchild ↑ .M + Rightchild ↑ .M 該結點為內部結點且 Count=0連續段數
這里的連續段數指的是區間的并可以分解為多少個獨立的區間。如 [1 , 2] ∪[2,3]∪ [5 , 6] 可以分解為兩個區間[1 , 3] 與 [5 , 6] ,則連續段數為 2 。增加1個數據域 Lines_Tree.line 表示該結點的連續段數。 Line 的討論比較復雜,內部結點不能簡單地將左右孩子的 Line 相加。所以再增加 Lines_Tree.lbd 與 Lines_Tree.rbd 域。定義以下:
1 左端點 I 被描寫區間蓋到
lbd =
0 左端點 I 不被描寫區間蓋到
1 右端點 J 被描寫區間蓋到
rbd =
0 右端點 J 不被描寫區間蓋到
lbd 與 rbd 的實現:
1 該結點 count > 0
lbd = 0 該結點是葉結點且 count = 0
leftchild ↑ .lbd 該結點是內部結點且 Count=0
1 該結點 count > 0
rbd = 0 該結點是葉結點且 count = 0
rightchild ↑ .rbd 該結點是內部結點且 Count=0
有了 lbd 與 rbd , Line 域就能夠定義了:
1 該結點 count > 0
Line = 0 該結點是葉結點且 count =0
Leftchild ↑ .Line + Rightchild ↑.Line - 1 當該結點是內部結點且 Count=0 , Leftchild ↑ .rbd = 1 且 Rightchild ↑ .lbd = 1
Leftchild ↑.Line + Rightchild ↑ .Line 當該結點是內部結點且 Count=0 , Leftchild ↑ .rbd 與 Rightchild ↑ .lbd 不都為1
6.2 利用線段樹實現區間的動態插入和刪除
6.2.1 實例
PKU JudgeOnline, 1151, Atlantis.
6.2.2 問題描寫
在2維平面分部著1些矩形,矩形有可能重合。求矩形的總面積。
6.2.3 分析
這個題在《算法藝術與信息學比賽》中第1章介紹數據結構時,講到線段樹的時候有解題分析。
用線段樹來記載縱向上是否是被覆蓋,用測度來表示區間中被覆蓋了多少長度。
為了下降復雜度,可以將坐標離散化,以下圖所示:

從左到右掃描長方形的左邊邊和右邊邊,如果是左邊邊則加入線段樹中,否則從線段書中刪除。同時用橫向掃描的距離乘以線段樹的測度,就得到了掃描過了的被覆蓋的面積。
本題和PKU JudgeOnline,1117, Picture題都對線段樹進行了擴大。本題只用到了測度的擴大,而1117題還用到了獨立線段數的擴大。
//離散化+ 線段樹+ 掃描線
//本題與JudgeOnline 1177 picture 極類似,現在回想起來乃至比1177 還要簡單1些.與1177 不同的是本題中的坐標是浮點
//類型的故不能將坐標直接離散.我們必須為它們建立1個對應關系,用1個整數去對應1個浮點數
//這樣的對應關系在本題的數組y[] 中
#include<iostream>
#include<algorithm>
#include<cmath>
#include<iomanip>
using namespace std;
struct node{
int st, ed,c; //c : 區間被覆蓋的層數,m: 區間的測度
double m;
}ST[802];
struct line{
doublex,y1,y2; //縱方向直線, x:直線橫坐標, y1 y2:直線上的下面與上面的兩個縱坐標
bools; //s = 1: 直線為矩形的左側, s = 0:直線為矩形的右側
}Line[205];
double y[205],ty[205]; //y[] 整數與浮點數的對應數組;ty[]:用來求y[]的輔助數組
void build(int root, int st, int ed){
ST[root].st = st;
ST[root].ed = ed;
ST[root].c = 0;
ST[root].m = 0;
if(ed - st> 1){
int mid= (st+ed)/2;
build(root*2, st, mid);
build(root*2+1, mid, ed);
}
}
inline void updata(int root){
if(ST[root].c> 0)
//將線段樹上區間的端點分別映照到y[]數組所對應的浮點數上,由此計算出測度
ST[root].m = y[ST[root].ed⑴] -y[ST[root].st⑴];
else if(ST[root].ed - ST[root].st == 1)
ST[root].m = 0;
elseST[root].m = ST[root*2].m + ST[root*2+1].m;
}
void insert(int root, int st, int ed){
if(st <=ST[root].st && ST[root].ed <= ed){
ST[root].c++;
updata(root);
return;
}
if(ST[root].ed- ST[root].st == 1)return ;//不出錯的話這句話就是冗余的
int mid =(ST[root].ed + ST[root].st)/2;
if(st <mid)
insert(root*2, st, ed);
if(ed >mid)
insert(root*2+1, st, ed);
updata(root);
}
void Delete(int root, int st, int ed){
if(st <=ST[root].st && ST[root].ed <= ed){
ST[root].c--;
updata(root);
return;
}
if(ST[root].ed- ST[root].st == 1)return ; //不出錯的話這句話就是冗余的
int mid =(ST[root].st + ST[root].ed)/2;
if(st <mid)
Delete(root*2, st, ed);
if(ed >mid)
Delete(root*2+1, st, ed);
updata(root);
}
int Correspond(int n, double t){
//2分查找出浮點數t 在數組y[]中的位置(此即所謂的映照關系)
intlow,high,mid;
low = 0; high = n⑴;
while(low< high){
mid = (low+high)/2;
if(t> y[mid])
low = mid + 1;
elsehigh = mid;
}
returnhigh+1;
}
bool cmp(line l1, line l2){
return l1.x< l2.x;
}
int main()
{
intn,i,num,l,r,c=0;
doublearea,x1,x2,y1,y2;
while(cin>>n,n){
for(i =0; i < n; i++){
cin>>x1>>y1>>x2>>y2;
Line[2*i].x = x1; Line[2*i].y1 =y1; Line[2*i].y2 = y2; Line[2*i].s = 1;
Line[2*i+1].x = x2; Line[2*i+1].y1= y1; Line[2*i+1].y2 = y2; Line[2*i+1].s = 0;
ty[2*i] = y1; ty[2*i+1] = y2;
}
n <<= 1;
sort(Line, Line+n, cmp);
sort(ty, ty+n);
y[0] = ty[0];
//處理數組ty[]使之不含重覆元素,得到新的數組寄存到數組y[]中
for(i=num=1;i < n; i++)
if(ty[i]!= ty[i⑴])
y[num++] = ty[i];
build(1, 1, num); //樹的葉子結點與數組y[]中的元素個數相同,以便建立逐一對應的關系
area = 0;
for(i =0; i < n⑴; i++){
//由對應關系計算出線段兩端在樹中的位置
l = Correspond(num, Line[i].y1);
r = Correspond(num, Line[i].y2);
if(Line[i].s)//插入矩形的左側
insert(1, l, r);
else //刪除矩形的右側
Delete(1, l, r);
area += ST[1].m * (Line[i+1].x -Line[i].x);
}
cout<<"Testcase #"<<++c<<endl<<"Totalexplored area: ";
cout<<fixed<<setprecision(2)<<area<<endl<<endl;
}
return 0;
}
計算數組區間第K大的數
PKU JudgeOnline, 2761, Feed the dogs則是線段樹的另外1個利用:實用線段樹來計算數組區間[i, j]中元素第k小(或第K大)的數。只要添寫1個函數,根據線段樹中每一個結點的覆蓋樹木來判斷第k大的樹是哪個。
當初始化,或區間[i, j]產生變化時,需要對線段樹進行添加或刪除操作。每當增加(或刪除)1個大小為X的點時,就在樹上添加(或刪除)1條(X,MaxLen)的線段(不含端點),當要查詢1個點的排名時,只要看看其上有多少條線段就能夠了。
int query(int root, intcount)
{
if(count<= ST[root].c){
returnST[root].st;
}else if(ST[root].ed - ST[root].st == 1){
returnST[root].ed;
}
count -= ST[root].c;
if(count<= ST[root*2+1].c){
returnquery(root*2, count);
}else{
returnquery(root*2+1, count);
}
}
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈





