卡特蘭數

Catalan數的定義：

設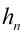表示用下面的方法把凸多邊形區域分成3角形區域的方法數：在有n+1條邊的凸多邊形區域內通過插入在其中不相交的對角線而把它分成3角形區域。定義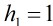。則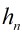滿足遞推關系

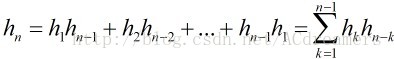
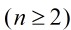
這個遞推關系的解是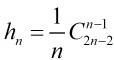：，這里的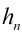叫做Catalan數。

那末上面的遞推式的正確性我們可以簡單描寫1下便可：

證明：這里由于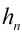表示依照上述規則劃分的3角形區域個數，那末我們隨意選1條多邊形的1條邊作為基邊，那末

     再在剩余的n⑴個點當選1個點，我們把所選的1條邊的兩點分別與所選的那1點連接起來，那末多邊形被劃

     分成3部份，1部份有k+1條邊，1部份有3條邊，另外一部份有n-k+1條邊，那末這樣就劃分成了子問題了，所

     以依照這個思路可以證明遞推式成立。

那末根據遞推式是如何推出Catalan數的通項公式呢？

這里用到了生成函數：我們很容易寫出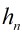的生成函數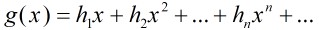

我們進1步計算

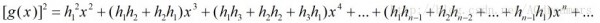
由于有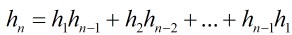：，所以進1步得到：

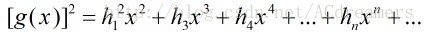，由于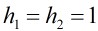

所以有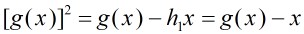：，解之得到：

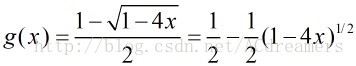，另外一個解不符合，舍去。

那末根據牛頓2項式有：

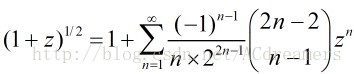
那末帶入化簡得到：

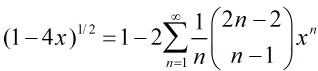
那末我們終究得到：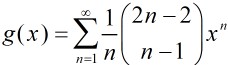

所以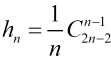：，這就是Catalan的推導進程。

卡特蘭數的利用

1、括號化問題

矩陣連乘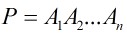：，根據乘法結合律，不改變其順序，只用括號表示成對的乘積，問有幾種括號化的方案？

2、出棧次序問題

1個棧(無窮大)的進棧序列為1,2,3,..n,有多少個不同的出棧序列?

類似問題

a、有2n個人排成1行進入劇院，入場費5元。其中只有n個人有1張5元鈔票，另外n人只有10元鈔票，劇院無其它鈔票，問有多少中方法使得只要有10元的人買票，售票處就有5元的鈔票找零？(將持5元者到達視作將5元入棧，持10元者到達視作使棧中某5元出棧)

b、n個1和n個0組成1個2n位的2進制數，要求從左到右掃描，0的累計數不小于1的累計數，求滿足條件的的數。

c、12個人排成兩排，每排必須是從矮到高排列，而且第2排比對應的第1排的人高，問排列方式有多少種？

我們先把這12個人從低到高排列,然后,選擇6個人排在第1排,那末剩下的6個肯定是在第2排.用0表示對應的人在第1排,用1表示對應的人在第2排,那末含有6個0,6個1的序列,就對應1種方案.

比如000000111111就對應著
           

第1排：0 1 2 3 4 5
第2排：6 7 8 9 10 11
010101010101就對應著
第1排：0 2 4 6 8 10
第2排：1 3 5 7 9 11問題轉換為，這樣的滿足條件的01序列有多少個。與情況b1樣。

3、給定節點組成2叉樹的問題

給定N個節點，能構成多少種形狀不同的2叉樹？

先取1個點作為頂點,然后左側順次可以取0至N⑴個相對應的,右側是N⑴到0個,兩兩配對相乘,就是h(0)*h(n⑴) + h(2)*h(n⑵) +  + h(n⑴)h(0)=h(n))能構成h（N）個

4.n*n棋盤從左下角走到右上角而不穿過主對角線的走法

5.n個+1和n個⑴構成的2n項序列，其部份和總滿足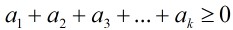：的序列的個數。

Catalan數的高精度處理：利用遞歸式： h(n)=((4*n⑵)/(n+1))*h(n⑴)

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈