區分于線性回歸,不是把每一個特點直接乘以系數,而是用1個S型函數(Logistic函數)。以下:
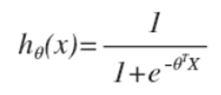
使用這類情勢函數的緣由(幾率、求導)。
代價函數,也不是線性回歸中的誤差平方和,而是基于對數似然函數,以下:
單個樣本的后驗幾率為: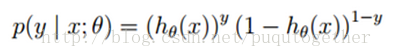 (y = 0, 1) 類似于2項散布的幾率密度函數。
(y = 0, 1) 類似于2項散布的幾率密度函數。
全部樣本集的后驗幾率:
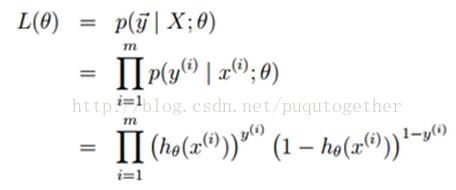
對數似然函數對代價函數,以下:
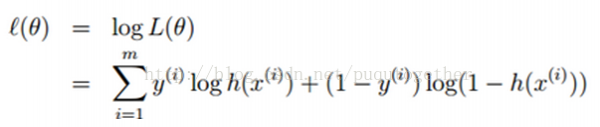
梯度降落法求解,對上面的代價函數求導,以下:
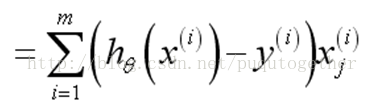
誤差乘以對應的屬性值,再求和。情勢和線性回歸1致,解釋了為什么設計這樣的S型函數和代價函數。這樣的梯度降落法的計算量簡單。
LR回歸的優點:計算量小,從梯度降落法求導公式可以看出;可以處理非線性數據。
缺點:容易產生過擬合。
如何避免過擬合:
(1) 降維,可使用PCA算法把樣本的維數下降,使得模型的theta的個數減少,次數也會下降,避免了過擬合;
(2) 正則化,設計正則項regularization term。
正則化作用就是避免某些屬性前的系數權重過大,出現過擬合。
注意LR回歸中解決過擬合的方式和決策樹中解決的方法不同。

上一篇 Erlang 印象