數據結構基礎(21) --DFS與BFS
來源:程序員人生 發布時間:2015-02-26 21:00:59 閱讀次數:3355次
DFS
從圖中某個頂點V0 動身,訪問此頂點,然后順次從V0的各個未被訪問的鄰接點動身深度優先搜索遍歷圖,直至圖中所有和V0有路徑相通的頂點都被訪問到(使用堆棧).
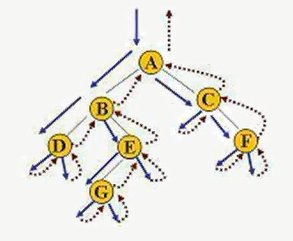
//使用鄰接矩陣存儲的無向圖的深度優先遍歷
template <typename Type>
void Graph<Type>::DFS()
{
stack<int> iStack;
showVertex(0);
vertexList[0]->wasVisted = true;
iStack.push(0);
while (!iStack.empty())
{
int top = iStack.top();
int v = getAdjUnvisitedVertex(top);
if (v == ⑴)
{
iStack.pop();
}
else
{
showVertex(v);
vertexList[v]->wasVisted = true;
iStack.push(v);
}
}
//使其還可以再深/廣度優先搜索
for (int i = 0; i < nVerts; ++i)
vertexList[i]->wasVisted = false;
}
BFS
從圖中的某個頂點V0動身,并在訪問此頂點以后順次訪問V0的所有未被訪問過的鄰接點,以后按這些頂點被訪問的前后次序順次訪問它們的鄰接點,直至圖中所有和V0有路徑相通的頂點都被訪問到.
若此時圖中尚有頂點未被訪問,則另選圖中1個未曾被訪問的頂點作起始點,重復上述進程,直至圖中所有頂點都被訪問到為止(使用隊列)。
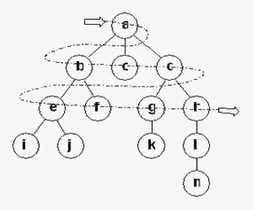
//使用鄰接矩陣存儲的無向圖的廣度優先遍歷
template <typename Type>
void Graph<Type>::BFS()
{
queue<int> iQueue;
showVertex(0);
vertexList[0]->wasVisted = true;
iQueue.push(0);
while (!iQueue.empty())
{
int front = iQueue.front();
iQueue.pop();
int v = getAdjUnvisitedVertex(front);
while (v != ⑴)
{
showVertex(v);
vertexList[v]->wasVisted = true;
iQueue.push(v);
v = getAdjUnvisitedVertex(front);
}
}
for (int i = 0; i < nVerts; ++i)
vertexList[i]->wasVisted = false;
}
附-完全代碼
const int MAX_VERTS = 20;
//頂點
template <typename Type>
class Vertex
{
public:
Vertex(const Type &_node = Type())
: node(_node), wasVisted(false) {}
public:
bool wasVisted; //增加1個訪問位
Type node;
};
//圖
template <typename Type>
class Graph
{
public:
Graph();
~Graph();
void addVertex(const Type &vertex);
void addEdge(int start, int end);
void printMatrix();
void showVertex(int v);
void DFS();
void BFS();
private:
int getAdjUnvisitedVertex(int v);
private:
Vertex<Type>* vertexList[MAX_VERTS];
int nVerts;
int adjMatrix[MAX_VERTS][MAX_VERTS];
};
template <typename Type>
void Graph<Type>::DFS()
{
stack<int> iStack;
showVertex(0);
vertexList[0]->wasVisted = true;
iStack.push(0);
while (!iStack.empty())
{
int top = iStack.top();
int v = getAdjUnvisitedVertex(top);
if (v == ⑴)
{
iStack.pop();
}
else
{
showVertex(v);
vertexList[v]->wasVisted = true;
iStack.push(v);
}
}
//使其還可以再深度優先搜索
for (int i = 0; i < nVerts; ++i)
vertexList[i]->wasVisted = false;
}
template <typename Type>
void Graph<Type>::BFS()
{
queue<int> iQueue;
showVertex(0);
vertexList[0]->wasVisted = true;
iQueue.push(0);
while (!iQueue.empty())
{
int front = iQueue.front();
iQueue.pop();
int v = getAdjUnvisitedVertex(front);
while (v != ⑴)
{
showVertex(v);
vertexList[v]->wasVisted = true;
iQueue.push(v);
v = getAdjUnvisitedVertex(front);
}
}
for (int i = 0; i < nVerts; ++i)
vertexList[i]->wasVisted = false;
}
//獲得下1個還沒有訪問的連通節點
template <typename Type>
int Graph<Type>::getAdjUnvisitedVertex(int v)
{
for (int j = 0; j < nVerts; ++j)
{
//首先是鄰接的, 并且是未訪問過的
if ((adjMatrix[v][j] == 1) &&
(vertexList[j]->wasVisted == false))
return j;
}
return ⑴;
}
//打印節點信息
template <typename Type>
void Graph<Type>::showVertex(int v)
{
cout << vertexList[v]->node << ' ';
}
template <typename Type>
Graph<Type>::Graph():nVerts(0)
{
for (int i = 0; i < MAX_VERTS; ++i)
for (int j = 0; j < MAX_VERTS; ++j)
adjMatrix[i][j] = 0;
}
template <typename Type>
Graph<Type>::~Graph()
{
for (int i = 0; i < nVerts; ++i)
delete vertexList[i];
}
template <typename Type>
void Graph<Type>::addVertex(const Type &vertex)
{
vertexList[nVerts ++] = new Vertex<Type>(vertex);
}
template <typename Type>
void Graph<Type>::addEdge(int start, int end)
{
//無向圖
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
template <typename Type>
void Graph<Type>::printMatrix()
{
for (int i = 0; i < nVerts; ++i)
{
for (int j = 0; j < nVerts; ++j)
cout << adjMatrix[i][j] << ' ';
cout << endl;
}
}
//測試代碼
int main()
{
Graph<char> g;
g.addVertex('A'); //0
g.addVertex('B'); //1
g.addVertex('C'); //2
g.addVertex('D'); //3
g.addVertex('E'); //4
g.addEdge(0, 1); //A-B
g.addEdge(0, 3); //A-D
g.addEdge(1, 0); //B-A
g.addEdge(1, 4); //B-E
g.addEdge(2, 4); //C-E
g.addEdge(3, 0); //D-A
g.addEdge(3, 4); //D-E
g.addEdge(4, 1); //E-B
g.addEdge(4, 2); //E-C
g.addEdge(4, 3); //E-D
g.printMatrix();
cout << "DFS: ";
g.DFS();
cout << "
BFS: ";
g.BFS();
return 0;
}
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈



