算法與數據結構基礎4:C++二叉樹實現及遍歷方法大全
來源:程序員人生 發布時間:2014-12-09 08:01:21 閱讀次數:2986次
binary search tree,中文翻譯為2叉搜索樹、2叉查找樹或2叉排序樹。簡稱為BST。
本文集齊了2叉樹的5大遍歷算法:先序遍歷、中序遍歷、后序遍歷、深度優先遍歷和廣度優先遍歷(同層遍歷也就是深度優先遍歷)。
// BSTree.h
#include <cstdio>
#include <iostream>
#include <stack>
#include <queue>
using namespace std;
// binary search tree,中文翻譯為2叉搜索樹、2叉查找樹或2叉排序樹。簡稱為BST
class BSTree
{
struct Node{
Node(int x = 0):data(x), lchild(NULL), rchild(NULL){}
struct Node* lchild;
struct Node* rchild;
int data;
};
public:
// **************************************************************************
// 類的4大函數:構造函數、拷貝構造函數、重載賦值運算符、析構函數
// **************************************************************************
BSTree();
~BSTree();
// **************************************************************************
// 增刪改查
// **************************************************************************
void Insert(int x);
// 返回2叉樹的個數
unsigned short Size();
unsigned short Deep();
unsigned short Leaf();
bool IsEmpty();
// 遍歷
void PreorderTraversal(); // 先序遍歷
void InorderTraversal(); // 中序遍歷
void PostorderTraversal(); // 后序遍歷
void DepthFirstSearch(); // 深度優先遍歷
void BreadthFirstSearch(); // 廣度優先遍歷
private:
// 遞歸計算2叉樹個數
unsigned short CountSize(Node* n);
unsigned short CountDeep(Node* n);
unsigned short CountLeaf(Node* n);
// 遞歸遍歷
void PreorderTraversal(Node* n);
void InorderTraversal(Node* n);
void PostorderTraversal(Node* n);
void DepthFirstSearch(Node* n);
void BreadthFirstSearch(Node* n);
void Free(Node* node);
private:
Node* m_root;
};
// **************************************************************************
// 私有方法
// **************************************************************************
unsigned short BSTree::CountSize(Node* n)
{
if(!n){
return 0;
}
return CountSize(n->lchild) + CountSize(n->rchild) + 1;
}
unsigned short BSTree::CountDeep(Node* n)
{
if (!n) {
return 0;
}
int ldeep = CountDeep(n->lchild);
int rdeep = CountDeep(n->rchild);
return ( ldeep > rdeep ) ? (ldeep + 1) : (rdeep + 1);
}
unsigned short BSTree::CountLeaf(Node* n)
{
if (!n){
return 0;
}
if (!n->lchild&& !n->rchild){
return 1;
}
return CountLeaf(n->lchild) + CountLeaf(n->rchild);
}
void BSTree::PreorderTraversal(Node* n)
{
if (n) {
cout << n->data << ",";
PreorderTraversal(n->lchild);
PreorderTraversal(n->rchild);
}
}
void BSTree::InorderTraversal(Node* n)
{
if (n) {
InorderTraversal(n->lchild);
cout << n->data << ",";
InorderTraversal(n->rchild);
}
}
void BSTree::PostorderTraversal(Node* n)
{
if (n) {
PostorderTraversal(n->lchild);
PostorderTraversal(n->rchild);
cout << n->data << ",";
}
}
void BSTree::DepthFirstSearch(Node* root)
{
stack<Node *> nodeStack;
nodeStack.push(root);
Node* node = NULL;
while(!nodeStack.empty()){
node = nodeStack.top();
cout << node->data << ",";
nodeStack.pop();
if (node->rchild) {
nodeStack.push(node->rchild);
}
if (node->lchild) {
nodeStack.push(node->lchild);
}
}
}
void BSTree::BreadthFirstSearch(Node* root)
{
queue<Node *> nodeQueue;
nodeQueue.push(root);
Node* node = NULL;
while(!nodeQueue.empty()){
node = nodeQueue.front();
nodeQueue.pop();
cout << node->data << ",";
if (node->lchild) {
nodeQueue.push(node->lchild);
}
if (node->rchild) {
nodeQueue.push(node->rchild);
}
}
}
void BSTree::Free(Node* n)
{
if (n) {
Free(n->lchild);
Free(n->rchild);
delete n;
n = NULL;
}
}
// **************************************************************************
// 類的4大函數:構造函數、拷貝構造函數、重載賦值運算符、析構函數
// **************************************************************************
BSTree::BSTree()
{
m_root = NULL;
}
BSTree::~BSTree()
{
Free(m_root);
}
// **************************************************************************
// 增刪改查
// **************************************************************************
void BSTree::Insert(int x)
{
Node* tmp = new Node(x);
if (!m_root){
m_root = tmp;
}
else{
Node* pre = m_root;
Node* cur = m_root;
while (cur){
pre = cur;
cur = (x < cur->data) ? (cur->lchild) : (cur->rchild);
}
(x < pre->data) ? (pre->lchild = tmp) : (pre->rchild = tmp);
}
}
unsigned short BSTree::Size()
{
return CountSize(m_root);
}
unsigned short BSTree::Deep()
{
return CountDeep(m_root);
}
unsigned short BSTree::Leaf()
{
return CountLeaf(m_root);
}
bool BSTree::IsEmpty()
{
return m_root == NULL;
}
void BSTree::PreorderTraversal()
{
PreorderTraversal(m_root);
cout << endl;
}
void BSTree::InorderTraversal()
{
InorderTraversal(m_root);
cout << endl;
}
void BSTree::PostorderTraversal()
{
PostorderTraversal(m_root);
cout << endl;
}
void BSTree::DepthFirstSearch()
{
DepthFirstSearch(m_root);
cout << endl;
}
void BSTree::BreadthFirstSearch()
{
BreadthFirstSearch(m_root);
cout << endl;
}
// mian.cpp
// test for BSTree
#include "BSTree.h"
#include <cstdlib>
#include <iostream>
using namespace std;
int main()
{
BSTree tree;
int arr[6] = {5, 4, 8, 1, 7, 10};
for (int i = 0; i < 6; ++i){
tree.Insert(arr[i]);
}
tree.PreorderTraversal();
tree.InorderTraversal();
tree.PostorderTraversal();
tree.DepthFirstSearch();
tree.BreadthFirstSearch();
cout << "size:" << tree.Size() << endl;
cout << "deep:" << tree.Deep() << endl;
cout << "leaf:" << tree.Leaf() << endl;
system("pause");
return 0;
}
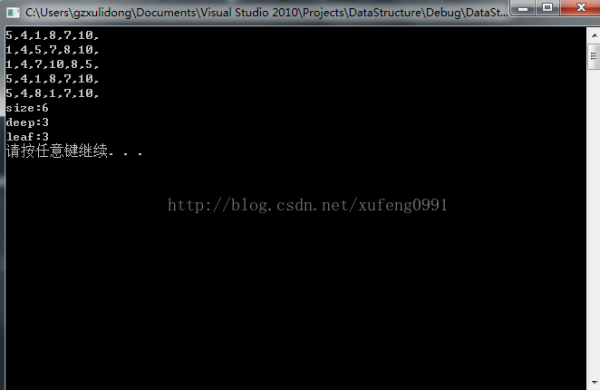
// 輸出截圖
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈


