《數據庫系統概論》---第二章 關系數據庫
來源:程序員人生 發布時間:2016-12-13 14:33:09 閱讀次數:4911次
1、概述
1.關系模型的組成
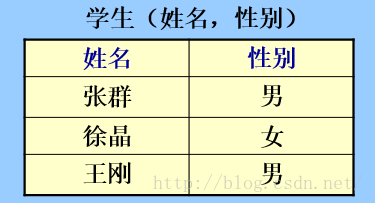
數據結構:2維表(關系),數據庫中全部數據和數據間的聯系都以關系來表示。
數據操作:增、刪、改、查
數據的束縛條件:實體完全性,參照完全性,用戶自定義的完全性。
2.關系的數據結構
域
·是1組既有相同數據類的值的集合,又稱值域。
·域中所包括值的個數稱為域的基數。
笛卡爾積
·所有域的所有取值的1個組合;不能重復
·笛卡爾積的表示方法
笛卡爾積可表示為1個2維表
表中的每行對應1個元祖,表中的每個列對應1個域
關系
R(D1,D2,...Dn)
R:關系名 n:關系的目或度
表的每行對應1個元組,表的每列對應1個域。由于域可以相同,為了加以辨別,必須對每列起1個名字,稱為屬性。n目關系必有n個屬性。
--元祖
關系中的元素是關系中的元祖,通經常使用t表示。
--關系的表示
關系也是1個2維表,表的每行對應1個組,表的每列對應1個域。
--屬性
關系中不同的列可以對應相同的域
3.定義關系模式
R(U, D, DOM, F)
R 關系名
U 組成該關系的屬性名集合
D 屬性組U中屬性所來自的域
DOM 屬性向域的映像集
F 屬性間的數據依賴關系
可簡記為 R(U) 或 R(A1,A2,...,An)
A1,A2,...,An 屬性名
關系模式
·關系模式是型,是穩定的
·關系是值 ,是動態的,隨時間不斷變化的
·關系模式是對關系的描寫
3類關系
·基本關系
實際存在的表,是實際存儲數據的邏輯表示
·查詢表
查詢結果對應的表
·視圖表
由基本表或其他視圖表導出的表,是虛表,不對應實際存儲的數據。
基本關系的性質
·列是同質的
·不同的列可出自同1個域,其中每個列稱為1個屬性,不同的屬性要給與不同的屬性名
·列的順序無所謂,列的次序可以交換
·任意兩個元祖的候選碼不能相同
·行的順序無所謂,行的次序可以交換
·份量必須取原子值
4.基本關系操作
查詢:選擇、投影、選擇、除、并、交、差
數據更新:插入、刪除、修改
查詢的表達能力是其中最重要的部份
選擇、投影、并、差、笛卡爾積是5種最基本的操作
關系操作的特點
集合操作方式:操作的對象和結果都是集合,1次1集合的方式
2、關系的完全性
碼
·候選碼
若關系中的某1屬性組的值能唯1地標識1個元組,則稱該屬性組為候選碼。
簡單的情況:候選碼只包括1個屬性
·全碼
最極真個情況:關系模式的所有屬性組是這個關系模式的候選碼,稱為全碼
·主碼
若1個關系有多個候選碼,則選定其中的1個作為主碼。每一個關系一定有且1個主碼。
·外碼
設F是基本關系R的1個或1組屬性,但不是關系R的碼。如果F與基本關系S的主碼Ks相對應,則稱F是基本關系R的外碼。
(基本關系R稱為參照關系;基本關系S稱為被參照關系或目標關系)
3類完全性束縛
實體完全性、參照完全性、用戶自定義完全性
1.實體完全性
實體完全性必須滿足
a.主屬性非空;b.主碼各不相同
2.參照完全性
如果關系R2的外碼F與R1的主碼p相對應,則R2中的每個元祖在F上的取值:
a.或為空值;b.或等于R1中某個元組的p值
3.用戶自定義的完全性
用戶針對具體的利用環境定義的完全性束縛條件。
例如:“成績”不能為負數,“性別”要求取值為“男”或“女”,“工齡”應當小于“年齡” 等。
3、關系代數
關系代數:將關系作為運算單位,用關系代數表達式表示的代數運算。
關系操作:傳統的集合運算和專門的關系運算
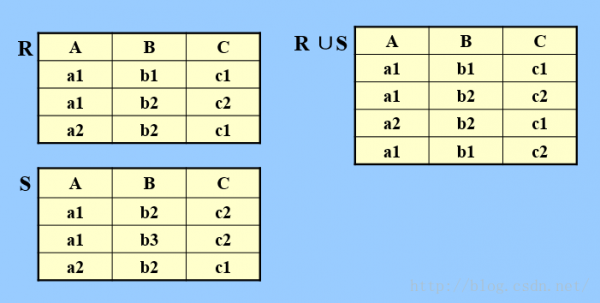
1.傳統的集合運算
除笛卡爾積外,要求參加運算的關系必須具有相容性。
定義:設給定兩個關系R、S,若滿足:
(1) 具有相同的度n,
(2) R中第i個屬性和S中第i個屬性來自同1個域,則說關系R、S是相容的。
a.并
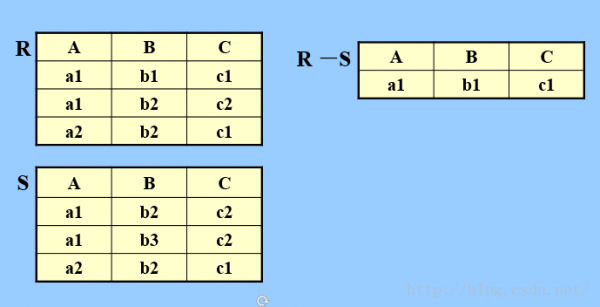
b.差
R和S具有相同的目n,相應的屬性取自同1個域。
R-S :仍為n目關系,由屬于R且不屬于S的元組組成。
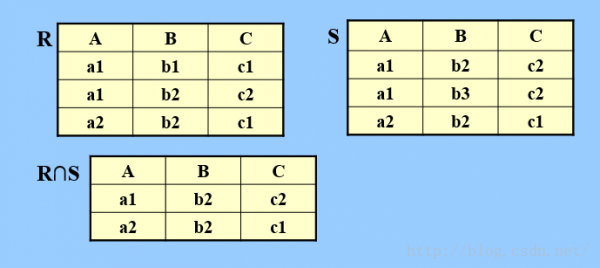
c.交
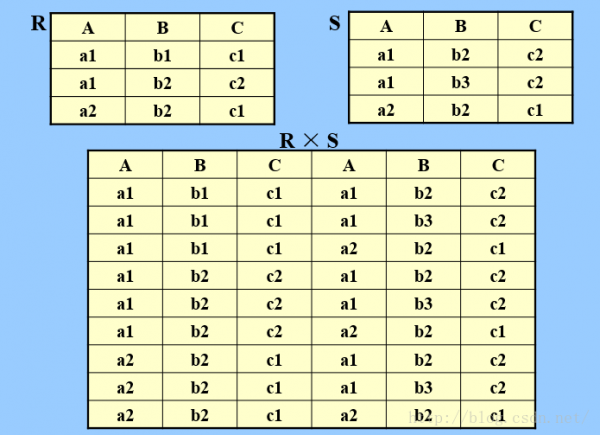
d.笛卡爾積 R X S
R:n目關系,k1個元組 S:m目關系,k2個元組
R X S:
列:(m+n)列元祖; 行:k1 X k2 個元組
2.專門的關系運算
a.選擇;
選擇操作是根據某些條件對關系做水平分割,即選取符合條件的元組構成結果關系。
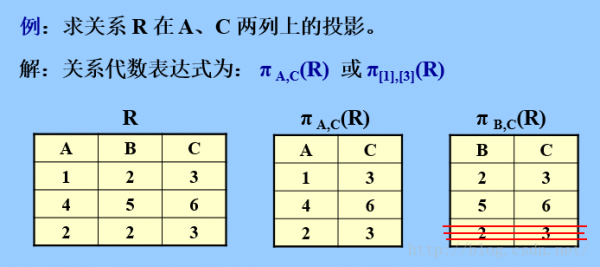
b.投影;
關系R上的投影是從R當選出若干屬性列組成新的關系。
·特點:
1) 在單個關系上進行
2) 從列的角度進行運算
3) 投影的列可按自己的要求的順序排列
·作用:
在關系當選擇某些需要的列,并按要求組成1個新關系。
注意:投影后取消了某些屬性列后,便可能出現重復行,應當刪除這些完全相同的行。所以投影以后,不但屬性減少了,元組也可能減少。
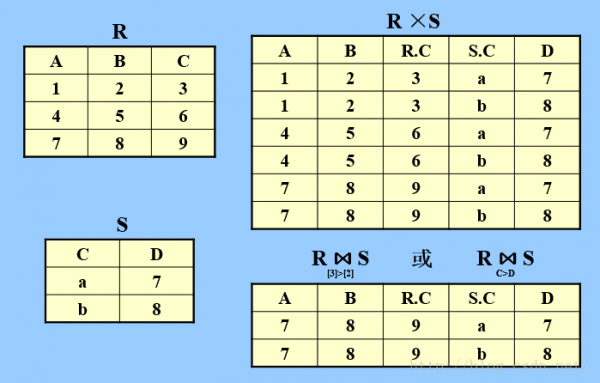
c.連接;
連接運算是從兩個關系的笛卡爾積當選取滿足連接條件的元組
記作:

其中A 和B 分別為 R 和 S 上度數相等且可比的屬性組。θ是比較運算符(> ≥ = < ≤ ≠)。
運算步驟:
1) 求笛卡爾積 R×S
2) 選擇其中滿足AθB的元組
特點:
1) 兩個關系參加運算,不1定有公共屬性
2) θ為“=”時,稱為等值連接
3) 結果關系中不去掉重復屬性
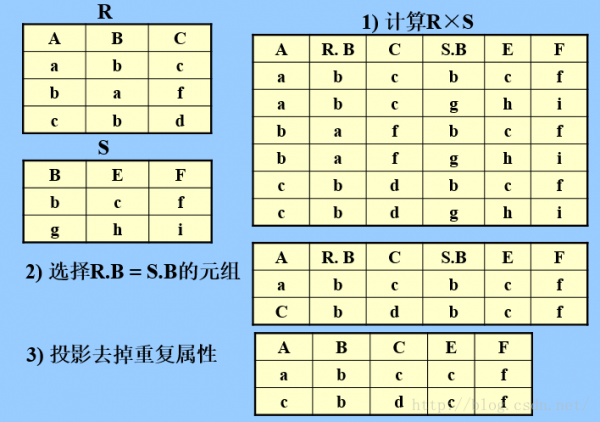
d.自然連接
自然連接與等值連接的區分:
自然連接中相等的份量必須是相同的屬性組,并且要在結果中去掉重復的屬性。
e.除法