Probability Latent Semantic Analysis (PLSA) 模型 學習筆記

Probability Latent Semantic Analysis (PLSA) 模型 學習筆記

    PLSA是前面LSA的兄弟版，相比于LSA而言，PLSA定義了幾率模型，而且每一個變量和相應的幾率散布和條件幾率散布都有明確的物理解釋了。這篇博文我們分3部份來講PLSA：基本思想，EM算法推導，和優缺點分析。

1.  PLSA的基本思想

    PLSA是1種主題模型topic model，是針對文本中隱含的主題來建模的方法。PLSA就是給定了文檔d以后，需要以1定的幾率選擇與文檔相對應的主題z，然后再從主題z中以1定的幾率選擇單詞w。我們用下圖來形象說明：

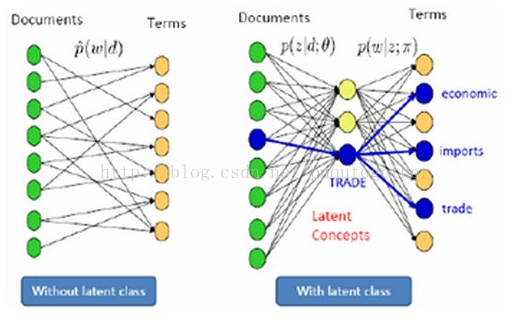
中間的那1層就是PLSA引入的“主題層”。其實從上面的介紹中你就能夠發現，PLSA是1種混合模型，需要使用兩層幾率（上面中兩處紅色標記）對全部樣本空間建模。下面的圖更加抽象地描寫了PLSA的模型：

    我們繼續使用1個例子來通俗理解PLSA的基本思想和它的利用：

    想象某個人要寫N篇文檔，他需要肯定每篇文檔里每一個位置上的詞。假定他1共有K個可選的主題，有V個可選的詞項，所以，他制作了K個V面的 “主題-詞項” 骰子，每一個骰子對應1個主題，骰子每面對應要選擇的詞項。然后，每寫1篇文檔會再制作1顆K面的 ”文檔-主題“ 骰子；每寫1個詞，先扔該骰子選擇主題；得到主題的結果后，使用和主題結果對應的那顆”主題-詞項“骰子，扔該骰子選擇要寫的詞。他不停的重復如上兩個扔骰子步驟，終究完成了這篇文檔。重復該方法N次，則寫完所有的文檔。在這個進程中，我們并未關注詞和詞之間的出現順序，所以PLSA也是1種詞袋方法；并且我們使用兩層幾率散布對全部樣本空間建模，所以PLSA也是1種混合模型。

    而真實的PLSA方法兩個“骰子”可能就不是均勻的，由于每一個主題的幾率不1定1樣，主題下每一個詞的幾率也不1定1樣。在PLSA模型中，我們需要做的就是如何求出這兩個幾率。

2. EM算法推導PLSA

    這部份網上講授的太多了，我選擇1個比較好懂，參考過來。（powered by Xinyan Lu）

3. PLSA的優缺點

    優點：PLSA可以解決了同義詞和多義詞的問題，利用了強化的期望最大化算法（EM）來訓練隱含類（潛伏類）。而且相對了LSA，有了堅實的統計學基礎。

    缺點：隨著document和term 個數的增加，pLSA模型也線性增加，變得愈來愈龐大，也就是說PLSA中訓練參數的值會隨著文檔的數目線性遞增。還有，PLSA可以生成其所在數據集的的文檔的模型，但卻不能生成新文檔的模型。

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈