您當前位置：首頁 > 互聯網 > [Java 8] Lambda表達式對遞歸的優化(下) - 使用備忘錄模式(Memoization Pattern)

[Java 8] Lambda表達式對遞歸的優化(下) - 使用備忘錄模式(Memoization Pattern)

來源：程序員人生發布時間：2014-11-17 08:24:43 閱讀次數：3609次

使用備忘錄模式(Memoization Pattern)提高性能

這個模式說白了，就是將需要進行大量計算的結果緩存起來，然后在下次需要的時候直接獲得就行了。因此，底層只需要使用1個Map就夠了。

但是需要注意的是，只有1組參數對應得到的是同1個值時，該模式才有用武之地。

在很多算法中，典型的比如分治法，動態計劃(Dynamic Programming)等算法中，這個模式應用的10分廣泛。以動態計劃來講，動態計劃在求最優解的進程中，會將原有任務分解成若干個子任務，而這些子任務必將還會將本身分解成更小的任務。因此，從整體而言會有相當多的重復的小任務需要被求解。明顯，當輸入的參數相同時，1個任務只需要被求解1次就行了，求解以后將結果保存起來。待下次需要求解這個任務時，會首先查詢這個任務是不是已被解決了，如果答案是肯定的，那末只需要直接返回結果就好了。

就是這么1個簡單的優化措施，常常能夠將代碼的時間復雜度從指數級的變成線性級。

以1個經典的桿切割問題(Rod Cutting Problem)(或這里也有更加正式的定義：維基百科)為例，來討論1下如何結合Lambda表達式來實現備忘錄模式。

首先，簡單交代1下這個問題的背景。

1個公司會批發1些桿(Rod)，然后對它們進行零售。但是隨著桿的長度不同，能夠賣出的價格也是不同的。所以該公司為了將利潤最大化，需要結合長度價格信息來決定應當將桿切割成甚么長度，才能實現利潤最大化。

比如，下面的代碼：

final List<Integer> priceValues = Arrays.asList(2, 1, 1, 2, 2, 2, 1, 8, 9, 15);

表達的意思是：長度為1的桿能夠賣2元，長度為2的桿能夠賣1元，以此類推，長度為10的桿能夠賣15元。

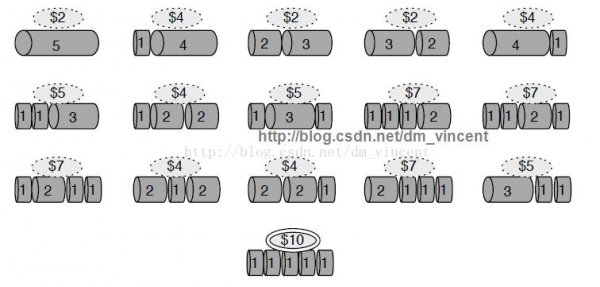
當需要被切割的桿長度為5時，存在的切割方法多達16種(2^(5 - 1))。以下所示：

針對這個問題，在不斟酌使用備忘錄模式的情況下，可使用動態計劃算法實現以下：

public int maxProfit(final int length) {
    int profit = (length <= prices.size()) ? prices.get(length - 1) : 0;
    for(int i = 1; i < length; i++) {
        int priceWhenCut = maxProfit(i) + maxProfit(length - i);
        if(profit < priceWhenCut) profit = priceWhenCut;
    }
    return profit;
}

而從上面的程序可以發現，有很多重復的子問題。對這些重復的子問題進行不斷糾結，損失了很多沒必要要的性能。分別取桿長為5和22時，得到的運行時間分別為：0.001秒和34.612秒。可見當桿的長度增加時，性能的降落時非常非常顯著的。

由于備忘錄模式的原理10分簡單，因此實現起來也很簡單，只需要在以上maxProfit方法的頭部加上Map的讀取操作并判斷結果就能夠了。但是這樣做的話，代碼的復用性會不太好。每一個需要使用備忘錄模式的地方，都需要單獨寫判斷邏輯，那末有無1種通用的辦法呢？答案是肯定的，通過借助Lambda表達式的氣力可以輕易辦到，以下代碼我們假定有1個靜態方法callMemoized用來通過傳入1個策略和輸入值，來求出最優解：

public int maxProfit(final int rodLenth) {
    return callMemoized(
        (final Function<Integer, Integer> func, final Integer length) -> {
        int profit = (length <= prices.size()) ? prices.get(length - 1) : 0;
        for(int i = 1; i < length; i++) {
            int priceWhenCut = func.apply(i) + func.apply(length - i);
            if(profit < priceWhenCut) profit = priceWhenCut;
        }
        return profit;
        }, rodLenth);
}

讓我們仔細分析1下這段代碼的意圖。首先callMemoized方法接受的參數類型是這樣的：

public static <T, R> R callMemoized(final BiFunction<Function<T,R>, T, R> function, final T input)

BiFunction類型的參數function實際上封裝了1個策略，其中有3個部份：

Function：通過傳入參數T，來得到解答R。這1點從代碼int priceWhenCut = func.apply(i) + func.apply(length - i)很明顯的就可以夠看出來。可以把它想象成1個備忘錄的入口。
T：代表求解問題時需要的參數T。
R：代表問題的答案R。

以上的T和R都是指的類型。

下面我們看看callMemoized方法的實現：

public class Memoizer {
    public static <T, R> R callMemoized(final BiFunction<Function<T,R>, T, R> function, final T input) {
        Function<T, R> memoized = new Function<T, R>() {
            private final Map<T, R> store = new HashMap<>();
            public R apply(final T input) {
                return store.computeIfAbsent(input, key -> function.apply(this, key));
            }
        };

        return memoized.apply(input);
    }
}

在該方法中，首先聲明了1個匿名Function函數接口的實現。其中定義了備忘錄模式的核心---Map結構。然后在它的apply方法中，會借助Java 8中為Map接口新添加的1個computeIfAbsent方法來完成下面的邏輯：

通過傳入的key檢查(在以上代碼中是input)對應的值是不是存在于備忘錄的底層Map中
如果存在，跳轉到步驟4
如果不存在，根據computeIfAbsent的第2個參數(是1個Lambda表達式)來計算得到key對應的value
返回得到的value

具體到該方法的源碼：

default V computeIfAbsent(K key, Function<? super K, ? extends V> mappingFunction) {
    Objects.requireNonNull(mappingFunction);
    V v;
    if ((v = get(key)) == null) {
        V newValue;
        if ((newValue = mappingFunction.apply(key)) != null) {
            put(key, newValue);
            return newValue;
        }
    }

    return v;
}

也能夠很清晰地看出以上的幾個步驟是如何體現在代碼中的。

關鍵的地方就在于第3步，如果不存在對應的value，那末需要調用傳入的Lambda表達式進行求解。以上代碼傳入的是key -> function.apply(this, key)，這里的this使用的10分奇妙，它實際上指向的就是這個用于容納Map結構的匿名Function實例。它作為第1個參數傳入到算法策略中，同時需要求解的key被當作第2個參數傳入到算法策略。這里所謂的算法策略，實際上就是在調用callMemoized方法時，傳入的情勢為BiFunction<Function<T,R>, T, R>的參數。

因此，所有的子問題僅僅會被求解1次。在得到子問題的答案以后，答案會被放到Map數據結構中，以便將來的使用。這就是借助Lambda表示實現備忘錄模式的方法。

以上的代碼可能會顯得有些奇異，這很正常。在你反復瀏覽它們后，并且經過自己的思考能夠重寫它們時，也就是你對Lambda表達式具有更深理解之時。

使用備忘錄模式后，桿長依然取5和22時，得到的運行時間分別為：0.050秒和0.092秒。可見當桿的長度增加時，性能并沒有如之前那樣降落的很利害。這完全是得益于備忘錄模式，此時所有的任務都只會被運行1次。

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈
程序員人生