一種快速開平方并取倒數算法
來源:程序員人生 發布時間:2014-11-15 06:44:43 閱讀次數:2643次
今天在查資料進程中,無意中看到這樣1段奇異的代碼,決定轉載到自己的csdn博客,但是找了半天,愣是沒找到csdn轉載功能,此前常常看到他人轉載文章,然后心里1直在想,是否是轉載是1個隱藏功能,或使用甚么命令就能夠了。因而特地谷歌了下,原來csdn的轉載功能,根本沒有甚么快速轉載、1鍵轉載,只有對著原文復制、粘貼,然后在自己的博客里面重新排版,最后在發布文章時選擇轉載,這樣該文章就成為1篇轉摘的文章了。這么設計也有道理,只有不嫌麻煩的人,才會耐心的完成轉載,算是提高了轉載的門坎,避免出現大量重復文章。不過,這么設計的副作用就是,浪費了很多時間和精力。吐槽就到這里,還是看看這段奇異的快速開平方并取倒數代碼:
float InvSqrt(float x )
{
float xhalf = 0.5f * x;
int i = *( int *)& x;
i = 0x5f3759df - ( i>>1);
x = *( float *)& i;
x = x * (1.5f - xhalf * x * x);
return x;
}
關于該段代碼的更多說明,請參看這篇文章《0x5f3759df的數學原理》。
下面為我編寫的簡單測試代碼:
#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <windows.h>
#include <math.h>
// 開平方取倒數
float InvSqrt(float x )
{
float xhalf = 0.5f * x;
int i = *( int *)& x;
i = 0x5f3759df - ( i>>1);
x = *( float *)& i;
x = x * (1.5f - xhalf * x * x);
return x;
}
int main()
{
// 比較精度
float val = 0.0f;
val = 1.0f;
printf("計算精度比較:
");
printf("輸入值: %f 快速算法: %f VC函數: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
val = 16.0f;
printf("輸入值: %f 快速算法: %f VC函數: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
val = 25.0f;
printf("輸入值: %f 快速算法: %f VC函數: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
val = 100.0f;
printf("輸入值: %f 快速算法: %f VC函數: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
printf("
計算性能比較:
");
int count = 1000000;
DWORD timeStart = 0, timeEnd = 0;
timeStart = GetTickCount();
for (int i = 0; i < count; i++)
{
val = InvSqrt(100.0f);
}
timeEnd = GetTickCount();
printf("快速算法耗時: %f
", (timeEnd - timeStart) * 0.001);
timeStart = GetTickCount();
for (int i = 0; i < count; i++)
{
val = 1.0f / sqrt(100.0f);
}
timeEnd = GetTickCount();
printf("VC函數耗時: %f
", (timeEnd - timeStart) * 0.001);
printf("
");
system("pause");
return 0;
}
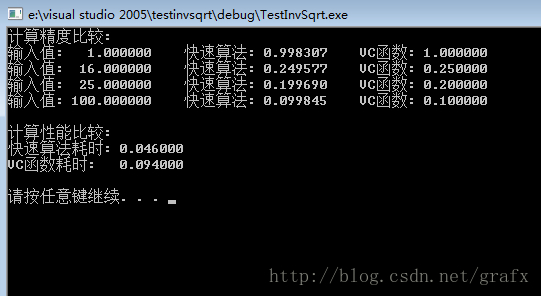
這里與sqrt()分別比較了計算精度及計算性能,測試環境為vs2005,普通pc筆記本(實際上是1臺年久的、玩的了游戲、寫得了代碼的小黑)。從對照結果看,該快速算法在計算結果上有1點點誤差,但是計算性能上很可觀。下圖為對照結果:
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈


