您當前位置：首頁 > 互聯網 > Codeforces Round #275 (Div. 2)

Codeforces Round #275 (Div. 2)

來源：程序員人生發布時間：2014-11-07 08:56:18 閱讀次數：2317次

鏈接:http://codeforces.com/contest/483

Your friend has recently learned about coprime numbers. A pair of numbers {a,?b} is called coprime if the maximum number that divides both a and b is equal to one.

Your friend often comes up with different statements. He has recently supposed that if the pair (a,?b) is coprime and the pair (b,?c) is coprime, then the pair (a,?c) is coprime.

You want to find a counterexample for your friend's statement. Therefore, your task is to find three distinct numbers (a,?b,?c), for which the statement is false, and the numbers meet the condition l?≤?a?<?b?<?c?≤?r.

More specifically, you need to find three numbers (a,?b,?c), such that l?≤?a?<?b?<?c?≤?r, pairs (a,?b) and (b,?c) are coprime, and pair (a,?c) is not coprime.

Input

The single line contains two positive space-separated integers l, r (1?≤?l?≤?r?≤?10¹⁸; r?-?l?≤?50).

Output

Print three positive space-separated integers a, b, c ― three distinct numbers (a,?b,?c) that form the counterexample. If there are several solutions, you are allowed to print any of them. The numbers must be printed in ascending order.

If the counterexample does not exist, print the single number ⑴.

Sample test(s)

Input

2 4

Output

2 3 4

Input

10 11

Output

⑴

Input

900000000000000009 900000000000000029

Output

900000000000000009 900000000000000010 900000000000000021

Note

In the first sample pair (2,?4) is not coprime and pairs (2,?3) and (3,?4) are.

In the second sample you cannot form a group of three distinct integers, so the answer is ⑴.

In the third sample it is easy to see that numbers 900000000000000009 and 900000000000000021 are divisible by three.

簡單構造：第1個數和第2個數互素，第2個數和第3個數互素，第1個數和第3個數不互素，明顯找偶奇偶序列

#include <cstdio> #define ll long long ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; } int main() { ll a, b; ll ans[3] = {0}; scanf("%I64d %I64d", &a, &b); if(b == a + 1) { printf("⑴ "); return 0; } if(a % 2 == 1) { ans[0] = a + 1; ans[1] = a + 2; } else { ans[0] = a; ans[1] = a + 1; } for(ll i = a + 2; i <= b; i++) { if(gcd(ans[1], i) == 1 && gcd(ans[0], i) != 1) { ans[2] = i; break; } } if(ans[2] == 0) { printf("⑴ "); return 0; } printf("%I64d %I64d %I64d ", ans[0], ans[1], ans[2]); }

You have two friends. You want to present each of them several positive integers. You want to present cnt₁ numbers to the first friend and cnt₂ numbers to the second friend. Moreover, you want all presented numbers to be distinct, that also means that no number should be presented to both friends.

In addition, the first friend does not like the numbers that are divisible without remainder by prime number x. The second one does not like the numbers that are divisible without remainder by prime number y. Of course, you're not going to present your friends numbers they don't like.

Your task is to find such minimum number v, that you can form presents using numbers from a set 1,?2,?...,?v. Of course you may choose not to present some numbers at all.

A positive integer number greater than 1 is called prime if it has no positive divisors other than 1 and itself.

Input

The only line contains four positive integers cnt₁, cnt₂, x, y (1?≤?cnt₁,?cnt₂?<?10⁹; cnt₁?+?cnt₂?≤?10⁹; 2?≤?x?<?y?≤?3?10⁴) ― the numbers that are described in the statement. It is guaranteed that numbers x, y are prime.

Output

Print a single integer ― the answer to the problem.

Sample test(s)

Input

3 1 2 3

Output

Input

1 3 2 3

Output

Note

In the first sample you give the set of numbers {1,?3,?5} to the first friend and the set of numbers {2} to the second friend. Note that if you give set {1,?3,?5} to the first friend, then we cannot give any of the numbers 1, 3, 5 to the second friend.

In the second sample you give the set of numbers {3} to the first friend, and the set of numbers {1,?2,?4} to the second friend. Thus, the answer to the problem is 4.

構造兩個序列，第1個序列要有cnt1個數且其中不能有x的倍數，第2個序列要有cnt2個數且其中不能有y的倍數。要求求出這兩個序列中的最大數的最小值。

如果答案是ans則ans＋1也滿足可以發現問題滿足2分做法的條件，cnt1個數為num - num / x，及1到num中不包括x倍數的數的個數，同理

cnt2個數為num - num / y，還有1點要注意的是必須滿足cnt1 + cnt2 <= num - num / (x * y)由于題目要求兩個集合中的元素不同，又由于x，y必定互素，所以cnt1和cnt2的和必須小于1到num中不包括(x * y)倍數的數的個數，不然兩個集合必定出現重復元素，然后2分num的值即可以得到終究答案。

#include <cstdio> int cal(int a, int b) { return a - a / b; } int main() { int cnt1, cnt2, x, y; scanf("%d %d %d %d", &cnt1, &cnt2, &x, &y); int l = 1, r = 2e9; while(l < r) { int mid = l + (r - l) / 2; if(cnt1 <= cal(mid, x) && cnt2 <= cal(mid, y) && cnt1 + cnt2 <= cal(mid, x * y)) r = mid; else l = mid + 1; } printf("%d ", r); }

Permutation p is an ordered set of integers p₁,???p₂,???...,???p_n, consisting of n distinct positive integers not larger than n. We'll denote as n the length of permutation p₁,???p₂,???...,???p_n.

Your task is to find such permutation p of length n, that the group of numbers |p₁?-?p₂|,?|p₂?-?p₃|,?...,?|p_n?-?1?-?p_n| has exactly k distinct elements.

Input

The single line of the input contains two space-separated positive integers n, k (1?≤?k?<?n?≤?10⁵).

Output

Print n integers forming the permutation. If there are multiple answers, print any of them.

Sample test(s)

Input

3 2

Output

1 3 2

Input

3 1

Output

1 2 3

Input

5 2

Output

1 3 2 4 5

Note

By |x| we denote the absolute value of number x.

1個包括n個數的數列，要求相鄰兩元素差的絕對值的數的個數為k，要求構造這樣的數列。

簡單的構造題，k－－并變號判斷便可

#include <cstdio> #include <cstring> int const MAX = 1e5 + 5; int a[MAX]; int hash[MAX]; int main() { int n, k; scanf("%d %d", &n, &k); memset(hash, 0, sizeof(hash)); a[1] = 1; hash[a[1]] = 1; int cnt = 1; for(int i = 2; i <= n; i++) { cnt++; a[i] = a[i - 1] + k; hash[a[i]] = 1; if(k > 0) k--; else k++; k *= ⑴; if(k == 0) break; } for(int i = 1; i <= n; i++) if(!hash[i]) a[++cnt] = i; for(int i = 1; i < n; i++) printf("%d ", a[i]); printf("%d ", a[n]); }

We'll call an array of n non-negative integers a[1],?a[2],?...,?a[n] interesting, if it meets m constraints. The i-th of the m constraints consists of three integers l_i, r_i, q_i (1?≤?l_i?≤?r_i?≤?n) meaning that value 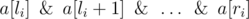$\text{[math]}$ should be equal to q_i.

Your task is to find any interesting array of n elements or state that such array doesn't exist.

Expression x&y means the bitwise AND of numbers x and y. In programming languages C++, Java and Python this operation is represented as "&", in Pascal ― as "and".

Input

The first line contains two integers n, m (1?≤?n?≤?10⁵, 1?≤?m?≤?10⁵) ― the number of elements in the array and the number of limits.

Each of the next m lines contains three integers l_i, r_i, q_i (1?≤?l_i?≤?r_i?≤?n, 0?≤?q_i?<?2³⁰) describing the i-th limit.

Output

If the interesting array exists, in the first line print "YES" (without the quotes) and in the second line print n integers a[1],?a[2],?...,?a[n] (0?≤?a[i]?<?2³⁰) decribing the interesting array. If there are multiple answers, print any of them.

If the interesting array doesn't exist, print "NO" (without the quotes) in the single line.

Sample test(s)

Input

3 1
1 3 3

Output

YES
3 3 3

Input

3 2
1 3 3
1 3 2

Output

NO

題意如題，還是構造數列，線段樹保護＋判斷

#include <cstdio> #include <cstring> #include <vector> using namespace std; int const MAX = 110000; struct Node { int l, r; int val; }; Node tree[10 * MAX]; Node a[MAX]; vector<int> ans; void build(int step, int l, int r) { tree[step].l = l; tree[step].r = r; tree[step].val = 0; if(l == r) return; int mid = (l + r) >> 1; build(step << 1, l, mid); build(((step << 1) + 1), mid+1, r); } void update(int step, int l, int r, int val) { if(tree[step].l == l && tree[step].r == r) { tree[step].val |= val; return; } int mid = (tree[step].l + tree[step].r) >> 1; if(r <= mid) update(step << 1, l, r, val); else if(l > mid) update((step << 1) + 1, l, r, val); else { update(step << 1, l, mid, val); update((step << 1) + 1, mid+1, r, val); } } int query(int step, int l, int r) { if(tree[step].l == l && tree[step].r == r) return tree[step].val; int mid = (tree[step].l + tree[step].r) >> 1; if(r <= mid) return query(step << 1, l, r); if(l > mid) return query((step << 1) + 1, l, r); else return query(step << 1, l, mid) & query((step << 1) + 1, mid+1, r); } void solve(int step) { if(step != 1) tree[step].val |= tree[step >> 1].val; if(tree[step].l == tree[step].r) { ans.push_back(tree[step].val); return ; } solve(step << 1); solve((step << 1) + 1); } int main() { int n, m; scanf("%d %d", &n, &m); build(1, 1, n); for(int i = 0; i < m; i++) { scanf("%d %d %d", &a[i].l, &a[i].r, &a[i].val); update(1, a[i].l, a[i].r, a[i].val); } bool flag = true; for(int i = 0; i < m; i++) { if(query(1, a[i].l, a[i].r) != a[i].val) { flag = false; break; } } solve(1); if(flag) { printf("YES "); for(int i = 0; i < ans.size(); i++) printf("%d%c",ans[i], i == n ? ' ' : ' '); ans.clear(); printf(" "); } else printf("NO "); }

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈
程序員人生

------分隔線----------------------------

上一篇 Bash Shell 解析路徑獲取文件名和目錄名

下一篇 DNS查詢工具使用淺析：host、nslookup、dig

分享到:

------分隔線----------------------------

為碼而活

積分：4237

15粉絲

7關注

欄目熱點

多多色-多人伦交性欧美在线观看-多人伦精品一区二区三区视频-多色视频-免费黄色视屏网站-免费黄色在线

Codeforces Round #275 (Div. 2)