許鵬：從零開始學習，Apache Spark源碼走讀（三）

【編者按】在“ 許鵬：從零開始學習，Apache Spark源碼走讀（一）”及“ 專訪許鵬：談C程序員修養及大型項目源碼閱讀與學習”中，我們有對@徽滬一郎進行專訪，并分享了他對多個項目的源碼走讀文章，其中包括Storm及Spark（1-13）。本次我們將分享許鵬Spark源碼走讀系列的14、15兩篇，期間圖與數學的聯系章節非常值得參考，以下為博文：

---

免費訂閱“CSDN云計算”微信公眾號，實時掌握第一手云中消息！

CSDN作為國內最專業的云計算服務平臺，提供云計算、大數據、虛擬化、數據中心、OpenStack、CloudStack、Hadoop、Spark、機器學習、智能算法等相關云計算觀點，云計算技術，云計算平臺，云計算實踐，云計算產業資訊等服務。

---

Graphx實現剖析

概要

圖的并行化處理一直是一個非常熱門的話題，這里頭的重點有兩個，一是如何將圖的算法并行化，二是找到一個合適的并行化處理框架。Spark作為一個非常優秀的并行處理框架，集成了一些并行化的算法也是理所當然。

Graphx是一些圖的常用算法在Spark上的并行化實現，同時提供了豐富的API接口。本文就Graphx的代碼架構及PageRank在Graphx中的具體實現做一個初步的學習。

Google為什么贏得了搜索引擎大戰

當Google還在起步的時候，在搜索引擎領域，Yahoo!正如日中天，紅的發紫。顯然，在Google面前的是一堵讓人幾乎沒有任何希望的墻。但世事難料，現在“外事問谷歌”成了不爭的事實。

這種轉換到底是如何形成的了，有一個因素是這樣的，那就是Google發明了顯著提高搜索準確率的PageRank算法。如果說PageRank算法的提出讓谷歌牢牢站穩了搜索引擎大戰的腳跟，這是毫不夸張的。個人認為，搜索引擎有幾個要考慮的關鍵因素：

1. 要想吸引用戶，就必須要有出色的搜索準確率
2. 有了用戶，才能做廣告投放，提高廣告投放的針對性就可以盈利

上述兩個方面都有非常優秀的算法。

廢話少述，回到正題。PageRank算法是圖論的一個具體應用，下面轉到圖論。

圖論簡介

圖的組成

離散數學中非常重要的一個部分就是圖論，下面是一個無向連通圖

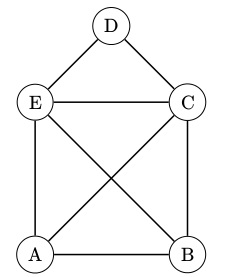
頂點（vertex）

上圖中的A、B、C、D、E稱為圖的頂點。

邊

頂點與頂點之間的連線稱之為邊。

圖的數學表示

讀大學的時候，一直沒有想明白為什么要學勞什子的線性代數。直到這兩天看《數學之美》一書時，才發覺，線性代數在一些計算機應用領域，那簡直就是不可或缺啊。

我們比較容易理解的平面幾何和立體幾何（一個是二維，一個是三維），而線性代數解決的其實是一個高維問題，由于無法直覺的感受到，所以很難。如果想比較通俗的理解一下數學為什么有這么多的分支及其內在關聯，強烈推薦讀一下《數學橋對高等數學的一次觀賞之旅》。

在數學中，用什么來表示圖呢，答案就是線性代數里面的矩陣，想想看，圖的關聯矩陣，圖的鄰接矩陣。總之就是矩陣，線性代數一下子有用了。下面是一個具體的例子。

圖的并行化處理

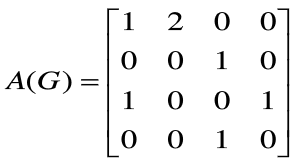
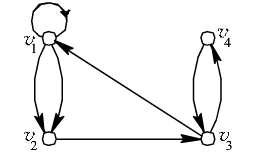
剛才說到圖可以用矩陣來表示，圖的并行化問題在某種程度上就被轉化為矩陣運算的并行化問題。那么以矩陣的乘法為例，看看其是否可以并行化處理。以矩陣 A X B 為例，說明并行化處理過程。

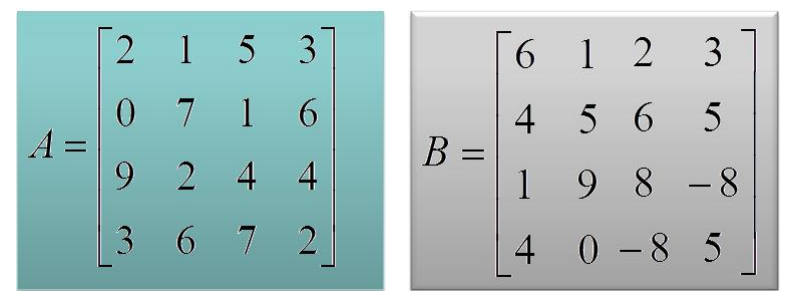
將上述的矩陣A和B劃分為四個部分，如下圖所示

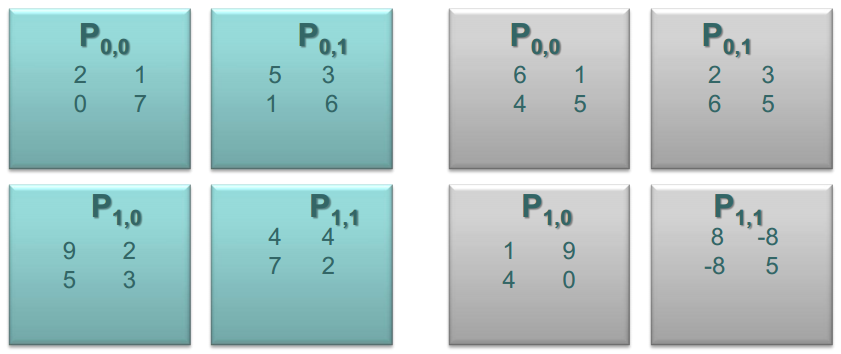
首次對齊之后

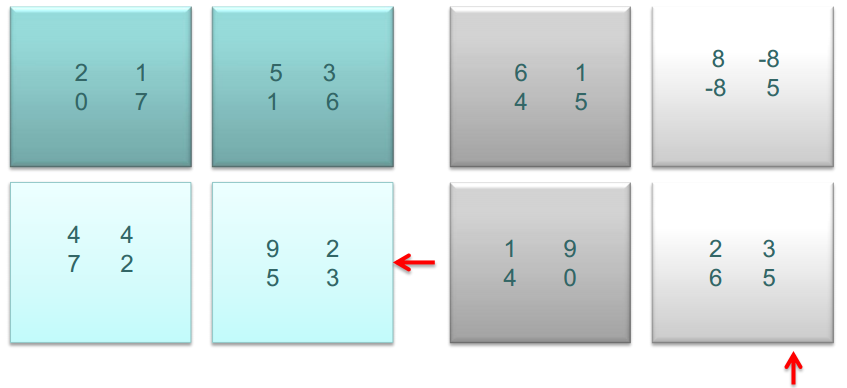
子矩陣相乘

相乘之后，A的子矩陣左移，B的子矩陣上移

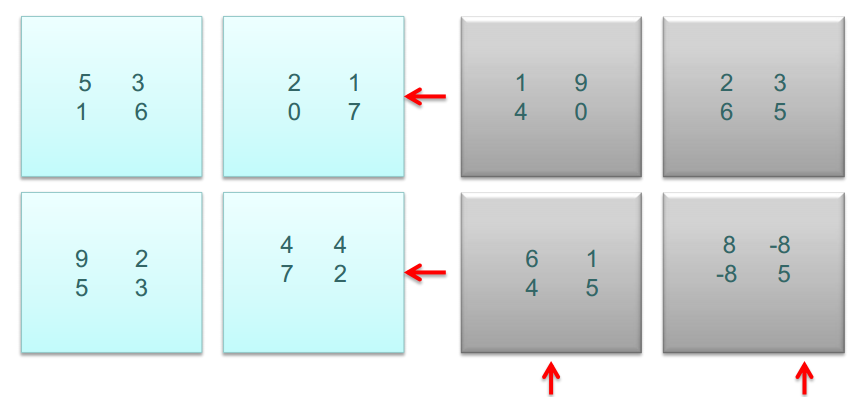
計算結果合并

圖的并行化處理框架，從Pregel說起。上一節的重點有兩點：

• 圖用矩陣來表示，對圖的運算就是矩陣的運算
• 矩陣乘法運算可以并行化，動態演示其并行化的原理

那有沒有一種合適的并行化處理框架可以用來進行圖的計算呢？那你肯定想到了MapReduce。MapReduce盡管也是一個不錯的并行化處理框架，但在圖計算方面，有許多缺點，主要是計算的中間過程需要存儲到硬盤，效率很低。Google針對圖的并行處理，專門提出了一個了不起的框架Pregel。其執行時的動態視圖如下所示。Pregel有如下優點：

• 級聯可擴性好，即Scalability
• 容錯性強
• 能夠很好的表示各種圖的常用算法

Pregel的計算模型

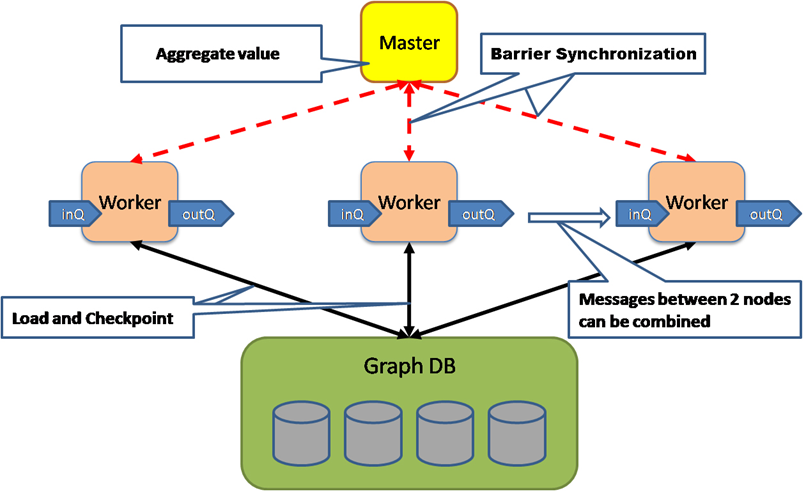
計算模型如下圖所示，重要的有三個

1. 作用于每個頂點的處理邏輯 vertexProgram
2. 消息發送，用于相鄰節點間的通訊 sendMessage
3. 消息合并邏輯 messageCombining

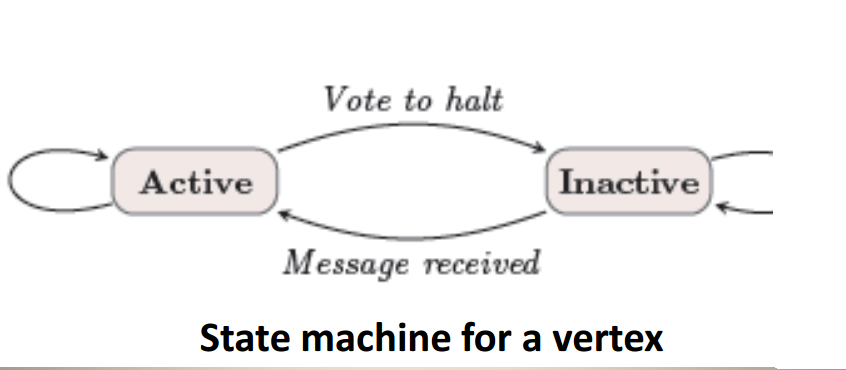
Pregel在Spark中的實現

非常感謝你能堅持看到現在，這篇博客內容很多，有點難。我想還是上一幅圖將其內在邏輯整一下再繼續說下去。

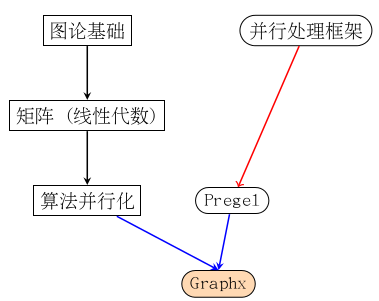
該圖要表示的意思是這樣的，Graphx利用了Spark這樣了一個并行處理框架來實現了圖上的一些可并行化執行的算法。本篇博客要表達的意思就是上面加紅的這句話，請諸位看官仔細理解。

• 算法是否能夠并行化與Spark本身無關
• 算法并行化與否的本身，需要通過數學來證明
• 已經證明的可并行化算法，利用Spark來實現會是一個錯的選擇，因為Graphx支持pregel的圖計算模型

Graphx中的重要概念

Graph

毫無疑問，圖本身是graphx中一個非常重要的概念。

成員變量

Graph中重要的成員變量分別為

• vertices
• edges
• triplets

為什么要引入triplets呢，主要是和Pregel這個計算模型相關，在triplets中，同時記錄著edge和vertex. 具體代碼就不羅列了。

成員函數

函數分成幾大類

1. 對所有頂點或邊的操作，但不改變圖結構本身，如mapEdges、mapVertices
2. 子圖，類似于集合操作中的filter subGraph
3. 圖的分割，即paritition操作，這個對于Spark計算來說，很關鍵，正是因為有了不同的Partition，才有了并行處理的可能，不同的PartitionStrategy，其收益不同。最容易想到的就是利用Hash來將整個圖分成多個區域
4. outerJoinVertices 頂點的外連接操作

圖的運算和操作 GraphOps

圖的常用算法是集中抽象到GraphOps這個類中，在Graph里作了隱式轉換，將Graph轉換

GraphOps

implicit def graphToGraphOps[VD: ClassTag, ED: ClassTag]
      (g: Graph[VD, ED]): GraphOps[VD, ED] = g.ops

支持的操作如下

1. collectNeighborIds
2. collectNeighbors
3. collectEdges
4. joinVertices
5. filter
6. pickRandomVertex
7. pregel
8. pageRank
9. staticPageRank
10. connectedComponents
11. triangleCount
12. stronglyConnectedComponents

RDD

RDD是Spark體系的核心，那么Graphx中引入了哪些新的RDD呢，有倆，分別為

• VertexRDD
• EdgeRDD

較之EdgeRdd，VertexRDD更為重要，其上的操作也很多，主要集中于Vertex之上屬性的合并，說到合并就不得不扯到關系代數和集合論，所以在VertexRdd中能看到許多類似于sql中的術語，如

• leftJoin
• innerJoin
  

至于leftJoin、innerJoin、outerJoin的區別，建議谷歌一下，不再贅述。

Graphx場景分析

圖的存儲和加載

在進行數學計算的時候，圖用線性代數中的矩陣來表示，那么如何進行存儲呢？

學數據結構的時候，老師肯定說過好多的辦法，不再