數據結構第一回合：樹

         不管是數據結構導論中還是軟考中，樹都是一個很重要的部分，相對來講數據結構導論比軟考中要講的相對詳細，下面我就結合例題對這部分進行一下整合：

          總的來說，結構如下：

         概述部分都是一些基本概念和性質的闡釋，森林和二叉樹都特殊形式的樹，判定樹和哈弗曼樹本質作為樹的同時，也可以作為樹的應用，運用樹（包括二叉樹）的基本知識描述和解決一些實際的問題  。下面就依次來看：

一、二叉樹

       1. 【概況】

           二叉樹有滿，完全、非完全三種情況。所謂滿二叉樹就是一個子結點都不差，所有的位置該有的都有，如圖：

         這樣一個都不缺的是滿的，假設現在該二叉樹中缺少了4這一個子結點，那么就是完全二叉樹，而如果2、4存在，7或者5的位置空了，那么就由一個完全變成不完全了。

完全二叉樹和非完全二叉樹的區別就是：有缺失的那一層，子結點的存在是否連續。

       【例題分析】（出自《數據結構導論》125頁 填空第4題）

         已知完全二叉樹的第7層有20個結點，則整個完全二叉樹的葉子結點個數是______.

        [解析] ：因為是一個完全二叉樹，所以在樹的最后一層一定有缺失，也就是說結點的個數小于2 的（n-1）次方個。而第6層一 定是滿的，一共有32 個結點。而根據題意該

                        樹一共有7層，而且根據完全二叉樹的性質，這20個結點是第6層的10結點中的子結點數。而第六層剩下的22個結點都是葉子結點。

                        所以，該樹的葉子結點一共有20+22=42個。

 2、樹和二叉樹之間的轉換

         在這里咱們用圖說話，這里說的明白。

         1）先將樹上所有的兄弟進行連接，得到原圖右邊的圖：

         2）再保留每一層的兄弟結點中的第一個作為該層的左子樹結點，斷開C、D與根結點的連線，直接將B、C、D作為一條線，以B為中心順時針向旋轉45度角，這樣就得到下面的圖：

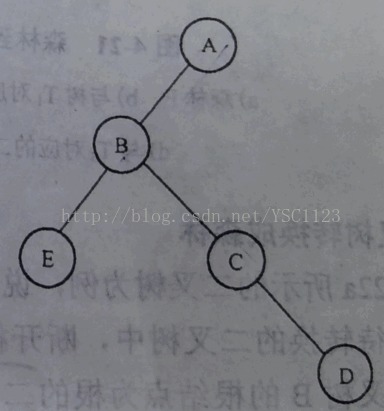
       其實可以這樣歸結：當所有的兄弟結點進行連線以后，每一層的所有兄弟結點中左邊的第一個都作為所有兄弟結點的父結點，其他的兄弟結點保持隊形，以該結點為中心進行旋轉，這樣就得出最終的二叉樹。

二、森林

         森林可以看作實實在在的樹的虛擬化，也是多棵樹組成的。這里知識點主要是和二叉樹之間的轉換

         森林和二叉樹之間的轉換實際上是對樹和二叉樹之間轉換的一種擴展，當將各個樹轉換為各自對應的二叉樹后，將所有的根結點作為兄弟進行連接，而實現二叉樹到森林的轉換就是一個逆過程，這里就不再贅述。

         這本數據結構第一遍看的挺亂，聽難的，翻開一看不是圖就是字母，頓時感覺全世界都被這兩個東西充斥了。但終究“眼是狗熊，手是英雄”，所以在學習的同時我總結了數據結構的一點學習技巧：

      1.實例化

            “此實例化非彼實例化”，這里主要是融入生活，用生活中常見的熟悉的事物來代替或者是幫助理解這些抽象的，空曠的理論結構。

      2.手腦并用            

              這門課中很多知識點都需要另外的思路圖來輔助理解，比如樹、圖、或者指針的指向。這就要求我們手腦并用，用紙上的圖來幫我們理解和解決。

      3.沉心

             面對那些龐雜的專業名詞，豐富的樹圖都不要畏懼，免得自己心沉。為了不讓自己心沉就必須沉心，要是能鬧明白這兩個詞，那你就"沉心"了:靜下心仔細想想好好理理，其實問題都不是問題。

          這門數據結構就是一個紙貓，因為它連老虎也不算，大家加油！

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈