信用評分卡模型在國外是一種成熟的預測方法,尤其在信用風險評估以及金融風險控制領域更是得到了比較廣泛的使用,其原理是將模型變量WOE編碼方式離散化之后運用logistic回歸模型進行的一種二分類變量的廣義線性模型。
Woe公式如下:
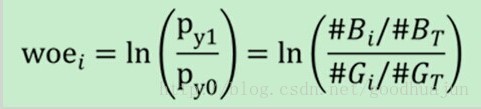
|
Age |
#bad |
#good |
Woe |
|
0-10 |
50 |
200 |
=ln((50/100)/(200/1000))=ln((50/200)/(100/1000)) |
|
10-18 |
20 |
200 |
=ln((20/100)/(200/1000))=ln((20/200)/(100/1000)) |
|
18-35 |
5 |
200 |
=ln((5/100)/(200/1000))=ln((5/200)/(100/1000)) |
|
35-50 |
15 |
200 |
=ln((15/100)/(200/1000))=ln((15/200)/(100/1000)) |
|
50以上 |
10 |
200 |
=ln((10/100)/(200/1000))=ln((10/200)/(100/1000)) |
|
匯總 |
100 |
1000 |
|
講完WOE下面來說一下IV:
IV公式如下:
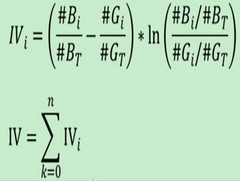
其實IV衡量的是某一個變量的信息量,從公式來看的話,相當于是自變量woe值的一個加權求和,其值的大小決定了自變量對于目標變量的影響程度;從另一個角度來看的話,IV公式與信息熵的公式極其相似。
事實上,為了理解WOE的意義,需要考慮對評分模型效果的評價。因為我們在建模時對模型自變量的所有處理工作,本質上都是為了提升模型的效果。在之前的一些學習中,我也總結了這種二分類模型效果的評價方法,尤其是其中的ROC曲線。為了描述WOE的意義,還真的需要從ROC說起。仍舊是先畫個表格。

數據來自于著名的German credit dataset,取了其中一個自變量來說明問題。第一列是自變量的取值,N表示對應每個取值的樣本數,n1和n0分別表示了違約樣本數與正常樣本數,p1和p0分別表示了違約樣本與正常樣本占各自總體的比例,cump1和cump0分別表示了p1和p0的累計和,woe是對應自變量每個取值的WOE(ln(p1/p0)),iv是woe*(p1-p0)。對iv求和(可以看成是對WOE的加權求和),就得到IV(information
value信息值),是衡量自變量對目標變量影響的指標之一(類似于gini,entropy那些),此處是0.666,貌似有點太大了,
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈

下一篇 對于UML圖的重新認識