在程序員的職業(yè)生涯中，算法亦算是一門(mén)基礎(chǔ)課程，尤其是在面試的時(shí)候，很多公司都會(huì)讓程序員編寫(xiě)一些算法實(shí)例，例如快速排序、二叉樹(shù)查找等等。
本文總結(jié)了程序員在代碼面試中最常遇到的10大算法類型，想要真正了解這些算法的原理，還需程序員們花些功夫。
1.String/Array/Matrix
在Java中，String是一個(gè)包含char數(shù)組和其它字段、方法的類。如果沒(méi)有IDE自動(dòng)完成代碼，下面這個(gè)方法大家應(yīng)該記住：
toCharArray() //get char array of a String Arrays.sort() //sort an array Arrays.toString(char[] a) //convert to string charAt(int x) //get a char at the specific index length() //string length length //array size substring(int beginIndex) substring(int beginIndex, int endIndex) Integer.valueOf()//string to integer String.valueOf()/integer to string
下面列出一些需要高級(jí)算法才能解決的經(jīng)典問(wèn)題：
2.鏈表
在Java中實(shí)現(xiàn)鏈表是非常簡(jiǎn)單的，每個(gè)節(jié)點(diǎn)都有一個(gè)值，然后把它鏈接到下一個(gè)節(jié)點(diǎn)。
class Node {
int val;
Node next;
Node(int x) {
val = x;
next = null;
}
}比較流行的兩個(gè)鏈表例子就是棧和隊(duì)列。
棧（Stack）
class Stack{
Node top;
public Node peek(){
if(top != null){
return top;
}
return null;
}
public Node pop(){
if(top == null){
return null;
}else{
Node temp = new Node(top.val);
top = top.next;
return temp;
}
}
public void push(Node n){
if(n != null){
n.next = top;
top = n;
}
}
}class Queue{
Node first, last;
public void enqueue(Node n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public Node dequeue(){
if(first == null){
return null;
}else{
Node temp = new Node(first.val);
first = first.next;
return temp;
}
}
}
值得一提的是，Java標(biāo)準(zhǔn)庫(kù)中已經(jīng)包含一個(gè)叫做Stack的類，鏈表也可以作為一個(gè)隊(duì)列使用（add()和remove()）。（鏈表實(shí)現(xiàn)隊(duì)列接口）如果你在面試過(guò)程中，需要用到棧或隊(duì)列解決問(wèn)題時(shí)，你可以直接使用它們。
在實(shí)際中，需要用到鏈表的算法有：
3.樹(shù)&堆
這里的樹(shù)通常是指二叉樹(shù)。
class TreeNode{
int value;
TreeNode left;
TreeNode right;
}
下面是一些與二叉樹(shù)有關(guān)的概念：
堆（Heap）是一個(gè)基于樹(shù)的數(shù)據(jù)結(jié)構(gòu)，也可以稱為優(yōu)先隊(duì)列（ PriorityQueue），在隊(duì)列中，調(diào)度程序反復(fù)提取隊(duì)列中第一個(gè)作業(yè)并運(yùn)行，因而實(shí)際情況中某些時(shí)間較短的任務(wù)將等待很長(zhǎng)時(shí)間才能結(jié)束，或者某些不短小，但具有重要性的作業(yè)，同樣應(yīng)當(dāng)具有優(yōu)先權(quán)。堆即為解決此類問(wèn)題設(shè)計(jì)的一種數(shù)據(jù)結(jié)構(gòu)。
下面列出一些基于二叉樹(shù)和堆的算法：
4.Graph
與Graph相關(guān)的問(wèn)題主要集中在深度優(yōu)先搜索和寬度優(yōu)先搜索。深度優(yōu)先搜索非常簡(jiǎn)單，你可以從根節(jié)點(diǎn)開(kāi)始循環(huán)整個(gè)鄰居節(jié)點(diǎn)。下面是一個(gè)非常簡(jiǎn)單的寬度優(yōu)先搜索例子，核心是用隊(duì)列去存儲(chǔ)節(jié)點(diǎn)。
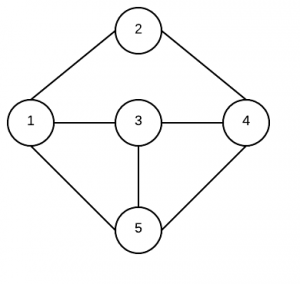
第一步，定義一個(gè)GraphNode
class GraphNode{
int val;
GraphNode next;
GraphNode[] neighbors;
boolean visited;
GraphNode(int x) {
val = x;
}
GraphNode(int x, GraphNode[] n){
val = x;
neighbors = n;
}
public String toString(){
return "value: "+ this.val;
}
}
第二步，定義一個(gè)隊(duì)列
class Queue{
GraphNode first, last;
public void enqueue(GraphNode n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public GraphNode dequeue(){
if(first == null){
return null;
}else{
GraphNode temp = new GraphNode(first.val, first.neighbors);
first = first.next;
return temp;
}
}
}第三步，使用隊(duì)列進(jìn)行寬度優(yōu)先搜索
public class GraphTest {
public static void main(String[] args) {
GraphNode n1 = new GraphNode(1);
GraphNode n2 = new GraphNode(2);
GraphNode n3 = new GraphNode(3);
GraphNode n4 = new GraphNode(4);
GraphNode n5 = new GraphNode(5);
n1.neighbors = new GraphNode[]{n2,n3,n5};
n2.neighbors = new GraphNode[]{n1,n4};
n3.neighbors = new GraphNode[]{n1,n4,n5};
n4.neighbors = new GraphNode[]{n2,n3,n5};
n5.neighbors = new GraphNode[]{n1,n3,n4};
breathFirstSearch(n1, 5);
}
public static void breathFirstSearch(GraphNode root, int x){
if(root.val == x)
System.out.println("find in root");
Queue queue = new Queue();
root.visited = true;
queue.enqueue(root);
while(queue.first != null){
GraphNode c = (GraphNode) queue.dequeue();
for(GraphNode n: c.neighbors){
if(!n.visited){
System.out.print(n + " ");
n.visited = true;
if(n.val == x)
System.out.println("Find "+n);
queue.enqueue(n);
}
}
}
}
}輸出結(jié)果：
value: 2 value: 3 value: 5 Find value: 5
value: 4
實(shí)際中，基于Graph需要經(jīng)常用到的算法：
5.排序
不同排序算法的時(shí)間復(fù)雜度，大家可以到wiki上查看它們的基本思想。
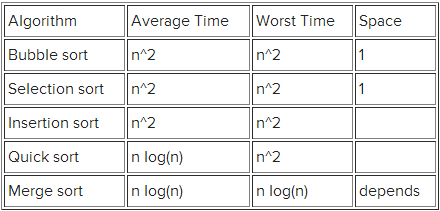
BinSort、Radix Sort和CountSort使用了不同的假設(shè)，所有，它們不是一般的排序方法。
下面是這些算法的具體實(shí)例，另外，你還可以閱讀： Java開(kāi)發(fā)者在實(shí)際操作中是如何排序的。
6.遞歸和迭代
下面通過(guò)一個(gè)例子來(lái)說(shuō)明什么是遞歸。
問(wèn)題：
這里有n個(gè)臺(tái)階，每次能爬1或2節(jié)，請(qǐng)問(wèn)有多少種爬法？
步驟1：查找n和n-1之間的關(guān)系
為了獲得n，這里有兩種方法：一個(gè)是從第一節(jié)臺(tái)階到n-1或者從2到n-2。如果f(n)種爬法剛好是爬到n節(jié)，那么f(n)=f(n-1)+f(n-2)。
步驟2：確保開(kāi)始條件是正確的
f(0) = 0;
f(1) = 1;
public static int f(int n){
if(n <= 2) return n;
int x = f(n-1) + f(n-2);
return x;
}
遞歸方法的時(shí)間復(fù)雜度指數(shù)為n，這里會(huì)有很多冗余計(jì)算。
f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(2) + f(2) + f(1)該遞歸可以很簡(jiǎn)單地轉(zhuǎn)換為迭代。
public static int f(int n) {
if (n <= 2){
return n;
}
int first = 1, second = 2;
int third = 0;
for (int i = 3; i <= n; i++) {
third = first + second;
first = second;
second = third;
}
return third;
}
在這個(gè)例子中，迭代花費(fèi)的時(shí)間要少些。關(guān)于迭代和遞歸，你可以去
這里看看。
7.動(dòng)態(tài)規(guī)劃
動(dòng)態(tài)規(guī)劃主要用來(lái)解決如下技術(shù)問(wèn)題：
上面所列的爬臺(tái)階問(wèn)題完全符合這四個(gè)屬性，因此，可以使用動(dòng)態(tài)規(guī)劃來(lái)解決：
public static int[] A = new int[100];
public static int f3(int n) {
if (n <= 2)
A[n]= n;
if(A[n] > 0)
return A[n];
else
A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
return A[n];
}
一些基于動(dòng)態(tài)規(guī)劃的算法：
8.位操作
位操作符：
從一個(gè)給定的數(shù)n中找位i（i從0開(kāi)始，然后向右開(kāi)始）
public static boolean getBit(int num, int i){
int result = num & (1<<i);
if(result == 0){
return false;
}else{
return true;
}
}
例如，獲取10的第二位：
i=1, n=10
1<<1= 10
1010&10=10
10 is not 0, so return true;典型的位算法：
9.概率
通常要解決概率相關(guān)問(wèn)題，都需要很好地格式化問(wèn)題，下面提供一個(gè)簡(jiǎn)單的例子：
有50個(gè)人在一個(gè)房間，那么有兩個(gè)人是同一天生日的可能性有多大？（忽略閏年，即一年有365天）
算法：
public static double caculateProbability(int n){
double x = 1;
for(int i=0; i<n; i++){
x *= (365.0-i)/365.0;
}
double pro = Math.round((1-x) * 100);
return pro/100;
}結(jié)果：
calculateProbability(50) = 0.97
10.組合和排列
組合和排列的主要差別在于順序是否重要。
例1：
1、2、3、4、5這5個(gè)數(shù)字，輸出不同的順序，其中4不可以排在第三位，3和5不能相鄰，請(qǐng)問(wèn)有多少種組合？
例2：
有5個(gè)香蕉、4個(gè)梨、3個(gè)蘋(píng)果，假設(shè)每種水果都是一樣的，請(qǐng)問(wèn)有多少種不同的組合？
基于它們的一些常見(jiàn)算法
來(lái)自：ProgramCreek
程序員人生，我編程，我富裕，記住wfuyu網(wǎng)，php教程，php學(xué)習(xí)，php手冊(cè)，CMS模版制作
聲明：本站大部分內(nèi)容是作者原創(chuàng)，少部分收集于互聯(lián)網(wǎng)供大家一起學(xué)習(xí)，原版權(quán)很多不明，如有侵權(quán)請(qǐng)聯(lián)系本站，謝謝！
粵ICP備14040726號(hào)-1?? 2015-2020 程序員人生 版權(quán)所有
