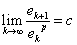【經典面試題】實現平方根函數sqrt
來源:程序員人生 發布時間:2014-09-09 07:17:22 閱讀次數:3889次
本文將從一道經典的面試題說起:實現平方根函數,不得調用其他庫函數。
函數原型聲明如下:
double Sqrt(double A);
二分法
二分法的概念
求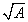 ,等價于求方程
,等價于求方程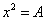 的非負根(解)。求解方程近似根的方法中,最直觀、最簡單的方法是二分法。“二分法”算法步驟如下:
的非負根(解)。求解方程近似根的方法中,最直觀、最簡單的方法是二分法。“二分法”算法步驟如下:
- 先找出一個區間 [a, b],使得f(a)與f(b)異號。
- 求該區間的中點 m = (a+b)/2,并求出 f(m) 的值。
- 若 f(m) * f(a) < 0 則取 [a, m] 為新的區間, 否則取 [m, b].
- 重復第2和第3步至理想精確度為止。
二分法的過程可用下圖表示:
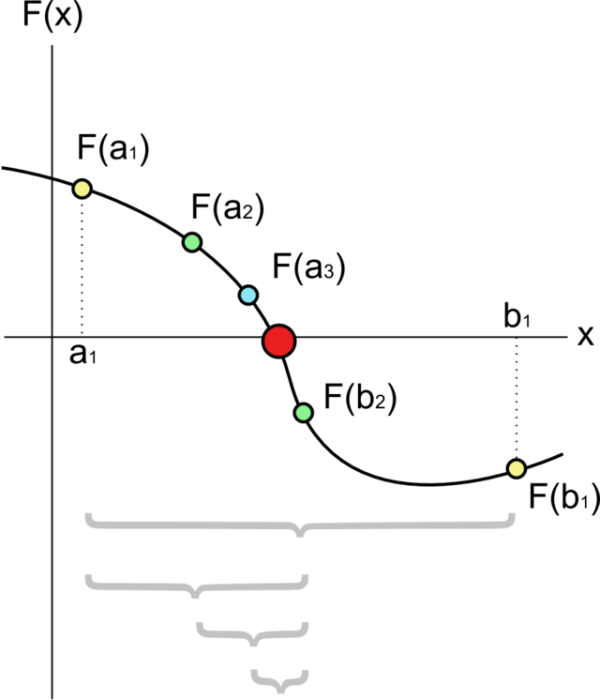
初始區間的選定
可見,若要用“二分法”求方程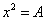 ,首先要找到一個區間 [a, b],使得f(a),f(b)異號。a可以取0,這很容易想到;但b如何選取,即如何選取b=f(A),使得
,首先要找到一個區間 [a, b],使得f(a),f(b)異號。a可以取0,這很容易想到;但b如何選取,即如何選取b=f(A),使得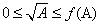 ?
?
取f(A)=A?不行,因為它不能始終保證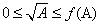 :
:
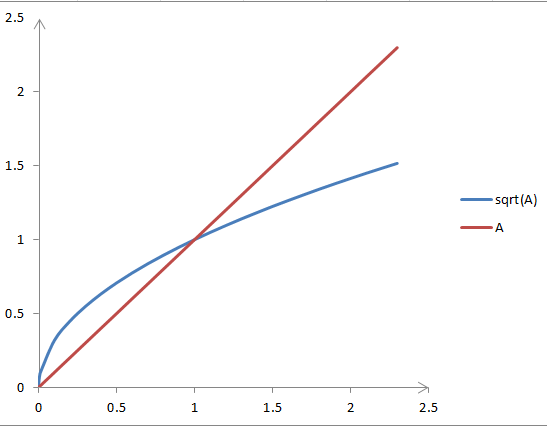
從圖像可知,當A>1時,才有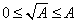 。若用A作為第一步的上界,則在A小于1時,將無法得到正確結果。
。若用A作為第一步的上界,則在A小于1時,將無法得到正確結果。
同時可知,sqrt(A)在原點處的切線平行于y軸,所以找不到常數項為零的多項式f(A),使得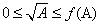 。
。
據此,可推出一個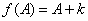 ,使得
,使得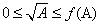 成立。
成立。
令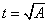 ,則t>=0,
,則t>=0,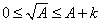 , 等價于
, 等價于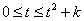 ,即
,即
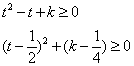
顯然,當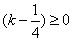 時,上式成立,所以k可以取[1/4, +∞)的任意值,不妨取k=1/4,即有
時,上式成立,所以k可以取[1/4, +∞)的任意值,不妨取k=1/4,即有
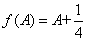 ,使得
,使得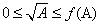 成立。
成立。
二分法的誤差
為了說明二分法的誤差,需要借助一個定理。
零點定理:若f(x)在(a,b)連續,且f(a)f(b)<0,則f(0)在(a, b)內有零點。
二分法每次迭代都能夠保證實際解在區間[a, b]范圍內,所以每次迭代的誤差都小于當前區間的寬度,這也是迭代的結束條件(通常誤差給定)。
二分法實現sqrt
根據以上分析,可以很快寫出sqrt的“二分法”版本:
double Sqrt(double A)
{
double a = 0.0, b = A + 0.25, m; // b = A 是錯誤的上界
// while(b - a > 2*DBL_EPSILON) { // sometimes dead cycle when m==a or m==b.
for(;;) {
m = (b + a)/2;
if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break;
if( (m*m - A) * (a*a - A) < 0 ) b = m;
else a = m;
}
return m;
}
需要注意的是:
- 初始上界是A+0.25,而不是A;
- double型的精度DBL_EPSILON,不能隨意指定;
牛頓迭代法
下面介紹另一種應用廣泛的方法――牛頓迭代法。
牛頓法的概念
牛頓迭代法是迭代法的一種,它的迭代格式為:
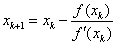
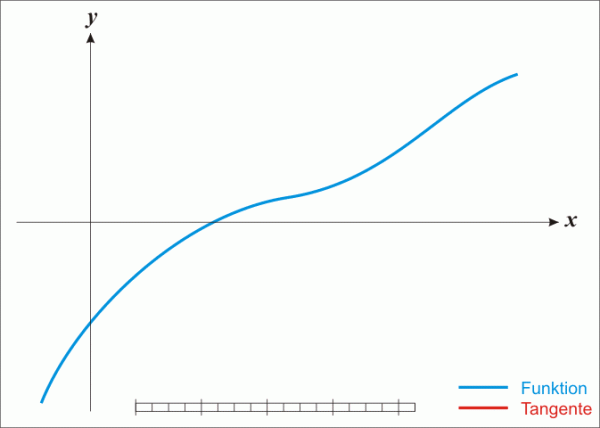
牛頓法具有明顯的幾何意義,x[k+1]正是曲線在x[k]處的切線與x軸的交點的橫坐標。因此,牛頓法也稱切線法。
來自Wikipedia的一個動態圖很好的解釋了這種幾何意義:
牛頓法初值的選定
在開始牛頓迭代法之前,需要選定一個d迭代初值x0。根據前文分析,求sqrt(A),也可以取x0 = A+0.25;
牛頓法sqrt
根據牛頓法,求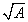 即求
即求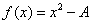 的非負根,
的非負根,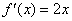 ,
,
所以,此時的牛頓遞推式為:
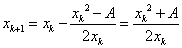
離實現牛頓法還差關鍵一步:迭代的結束條件。
在不知道誤差公式,且要求誤差盡可能小情況下可以使用另一種方法――限定f(x)=0的誤差(此法僅限于不給誤差范圍,且要求誤差盡可能小時使用)。
據此,實現的sqrt如下:
double Sqrt(double A)
{
double x0 = A + 0.25, x1, xx = x0;
for(;;) {
x1 = (x0*x0 + A) / (2*x0);
if(fabs(x1 - x0) <= DBL_EPSILON) break;
if(xx == x1) break; // to break two value cycle.
xx = x0;
x0 = x1;
}
return x1;
}
這段程序里的while條件是fabs(x1*x1-A) > 5*DBL_EPSILON是因為,x的誤差在2*DBL_EPSILON范圍內,所以x*x的誤差就在4*DBL_EPSILON范圍,考慮到浮點乘法的精度丟失,所以為5*DBL_EPSILON。
迭代法的理論基礎
迭代格式收斂的前提
迭代法在進行“迭代”之前,需將原方程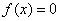 改寫成
改寫成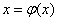 的形式;再用迭代格式
的形式;再用迭代格式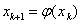 ,逐次逼近
,逐次逼近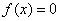 的實際解x*。
的實際解x*。
整個過程的所有x構成了數列: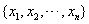 (迭代序列),數列的遞推式即
(迭代序列),數列的遞推式即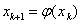 ;
;
所以,迭代法能夠求得近似解的前提是
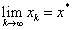
其中x*為方程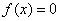 的實際解。
的實際解。
迭代格式收斂的條件
迭代法收斂的前提是 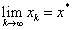 ,這很好理解;但要用此式驗證迭代式是否收斂,必須先通過遞推式
,這很好理解;但要用此式驗證迭代式是否收斂,必須先通過遞推式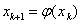 求出通項
求出通項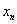 ;
;
是否有更簡單的方法判定迭代格式收斂?當然有,下面介紹一個定理能夠簡便的判定迭代格式是否收斂,同時也能判定誤差。
定理 迭代格式收斂條件(Vipschitz條件)
若迭代函數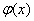 滿足:
滿足:
①一階導數連續;
②當x∈[a, b]時,有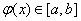 ;
;
③存在常數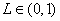 ,使得
,使得 ;
;
則
- 方程
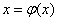 有唯一根x*;
有唯一根x*; - 對任意x0∈[a, b],迭代格式
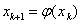 收斂,且
收斂,且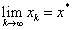 ;
; 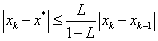 ,(事后誤差估計);
,(事后誤差估計);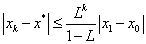 ,(事前誤差估計);
,(事前誤差估計);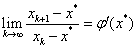
定理應用
下面以求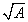 的近似解為例,說明定理如何用:
的近似解為例,說明定理如何用:
1)判斷收斂
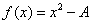 對應的迭代函數為:
對應的迭代函數為:
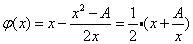
它的導函數為:
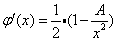
在[0, A+0.25]區間內它顯然連續,且存在L=1/2使得 ;
;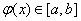 ;即滿足收斂的三個條件;
;即滿足收斂的三個條件;
2)估計誤差(迭代次數)
有了L = 1/2;就可以根據定理估算:
①給定誤差情況下,需要迭代幾次?
②給定迭代次數,最終近似解的誤差?
比如,假設題目要求的精度是:小數點后2位(精確到0.01),那么誤差要小于0.01 / 2 = 0.005;只需根據初值x0和第一次迭代結果x1和定理的結論4,便可算出迭代次數k,這里不再羅列(公式編輯起來比較麻煩)。
同樣,根據x0,x1和結論4,也可以很方便的算出第k次迭代的誤差;
推廣――一般方程求近似解
本文指出的二分法、牛頓迭代法是求解方程近似解的常見方法,不僅僅限于求sqrt,但在本文所實現的sqrt程序的基礎上,可以很快實現求解其他方程的程序。
二分法
比如,如下程序段就是二分法求解任意方程f(x)=0的程序:
double bisection(double (*f)(double), double a, double b, double eps)
{
double m;
assert( f != NULL && f(a) * f(b) < 0.0 && (b-a) > DBL_EPSILON); // (b-a) > DBL_EPSILON 即 b > a
while( b - a > eps ) {
m = (a + b)/2;
if( f(m) * f(a) < 0.0 ) b = m;
else a = m;
}
return m;
}
這個程序較為“好用”,只需給出函數f,區間[a, b],誤差eps即可。
迭代法
同樣,有了對迭代法的理論基礎,我們知道了迭代法的誤差如何估計。下面是迭代法求一般方程的近似解的程序:
double iteration(double (*g)(double), double L, double x0, double eps)
{
double x1, t = L/(1 - L);;
for(;;) {
x1 = g(x0);
if(fabs( t*(x1-x0) ) < eps)
break;
x0 = x1;
}
return x1;
}
這個函數沒有上面的二分法那么好用,因為需要根據f(x)自行推出遞推函數g,并根據遞推函數的倒數找到一個常數L;再給出初值x0,誤差eps。
割線法
事實上,真正通用的牛頓法很難實現,因為從f(x)推出它的導函數f1(x)的過程并不容易。割線法可以避免這一難題,它使用差商:
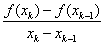
來代替牛頓公式中的導數f'(xk),于是得到了“割線法”迭代公式:
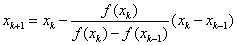
割線法和牛頓法類似,有著明確的幾何意義。下面的gif動態地展示了割線法的幾何意義(若沒有看到動畫效果可嘗試刷新本頁):
(圖片來自Dr. Mathews的教案,)
割線法求一般方程的近似解的程序如下:
double secant(double (*f)(double), double x0, double x1, double eps)
{
double x2;
for(;;) {
x2 = x1 - f(x1)/(f(x1) - f(x0))*(x1 - x0);
if( fabs(x2-x1) < eps )
break;
x0 = x1;
x1 = x2;
}
return x2;
}
這個函數也很好使用,只需給出f,[a, b],eps即可。
割線法實現的sqrt如下:
double Sqrt(double A)
{
double x0 = 0, x1 = A+0.25, x2;
double fx0 = x0*x0 - A, fx1 = x1*x1 - A;
for(;;) {
x2 = x1 - fx1*(x1-x0) / (fx1-fx0);
if(fabs(x2 - x1) < 2*DBL_EPSILON)
break;
x0 = x1; fx0 = fx1;
x1 = x2; fx1 = x2*x2 - A;
}
return x2;
}
收斂速度對比
對于sqrt的實現,本文介紹了三種方法,分別為:二分法,牛頓法,割線法;
二分法的收斂速度
對于二分法,相鄰兩次的誤差ek+1和ek間的關系為:
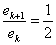 ,
,
由此,我們可以引申出迭代法收斂速度的判定標準:
定義 迭代法收斂的階
設序列{xk}收斂于x*,并記ek = xk - x*,如果存在非負常數c和正常數p,使得
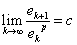
則稱序列{xk}是p階收斂的。當p=1,且0<|c|<1時,稱為線性收斂;當p>1時,稱超線性收斂,特別是p=2時,稱平方收斂。
由收斂階的定義可知,二分法是線性收斂的。
牛頓法的收斂速度
要確定牛頓法收斂的階,需要經過一番推導,限于篇幅,這里直接給出結論:
當x*是f(x)=0的單根(回顧一下二次方程)時,牛頓法至少是二階收斂的;
當x*是f(x)=0的重根時,牛頓法至少是一階收斂的。
割線法的收斂速度
分析割線法收斂的階同樣不易,它比牛頓法略慢一些;有知道的同學可以告訴我;
實驗對比
下面通過實驗對比幾種方法的收斂速度。實驗以不同版本的sqrt求出最終值所用的迭代次數為收斂速度的標準。
實驗程序如下:
#include <math.h> // for fabs sqrt
#include <float.h> // for DBL_EPSILON DBL_DIG etc.
#include <time.h> // for clock
#include <stdio.h>
#include <assert.h>
int iterateCount = 0;
double BisectionSqrt(double A)
{
double a = 0.0, b = A + 0.25, m;
for(;;){
m = (b + a)/2;
++iterateCount; // count iterate.
// printf(" %.15f
", m);
if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break;
if( (m*m - A) * (a*a - A) < 0.0 ) b = m;
else a = m;
}
return m;
}
double NewtonSqrt(double A)
{
double x0 = A + 0.25, x1, xx;
for(;;) {
x1 = (x0*x0 + A) / (2*x0);
++iterateCount; // count iterate.
// printf(" %.15f
", m);
if(fabs(x1 - x0) <= DBL_EPSILON) break;
if(xx == x1) return x0; // break two value cycle.
xx = x0;
x0 = x1;
}
return x1;
}
double SecantSqrt(double A)
{
double x0 = 0, x1 = A+0.25, x2;
double fx0 = x0*x0 - A, fx1 = x1*x1 - A;
for(;;) {
x2 = x1 - fx1*(x1-x0) / (fx1-fx0);
++iterateCount; // count iterate.
// printf(" %.15f
", x2);
if(fabs(x2 - x1) < 2*DBL_EPSILON)
break;
x0 = x1; fx0 = fx1;
x1 = x2; fx1 = x2*x2 - A;
}
return x2;
}
int main()
{
#ifdef F_INFO
puts("local machine floating point informations:");
printf("FLT_DIG: %d, %g
", FLT_DIG, FLT_EPSILON);
printf("LDBL_DIG: %d, %g
", DBL_DIG, DBL_EPSILON);
printf("LDBL_DIG: %d, %g
", LDBL_DIG, LDBL_EPSILON);
#endif
double x, res, stdres;
while( scanf("%lf", &x) == 1 )
{
stdres = sqrt(x);
printf("%15g ", x);
iterateCount = 0;
res = BisectionSqrt(x);
printf("%14g %3d ", res-stdres, iterateCount);
iterateCount = 0;
res = NewtonSqrt(x);
printf("%14g %3d ", res-stdres, iterateCount);
iterateCount = 0;
res = SecantSqrt(x);
printf("%14g %3d ", res-stdres, iterateCount);
printf("
");
}
return 0;
}
程序輸出 是為了方便重定位到文本文件后,粘貼到excel等表格軟件中;格式串是為了方便控制臺查看;
測試數據由下面的python腳本生成:
for x in range(1, 10000):
print x*0.01
for x in range(10000, 90000):
print x
for x in range(1000000, 9000000, 37):
print x
for x in range(100000000, 10000000000, 2311):
print x
可以通過管道進行測試:
gcc sqrt_cmp.c -o sqrt_cmp # 編譯
python inputgen_sqrt_cmp.py | sqrt_cmp # 測試
經過如下數據試驗:
delta = 0.05
count = 1/delta
for x in range(1, 2*int(count)):
print x*delta
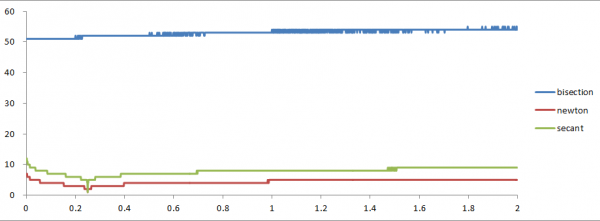
得到的迭代次數隨x的變化關系如下圖所示:
圖中,很坐標表示x值,縱坐標表示迭代次數。
試驗結果表明:牛頓法的收斂速度最快(迭代次數少),割線法次之,而二分法收斂最慢。
總結
本文分別描述了二分法、牛頓法、割線法,等幾種求方程近似解算法的步驟及實現;另外,從理論方面解釋了這些算法步驟背后數學原理;并將這些方法進行了一般化的推廣。最后,本文針對不同方法實現的sqrt進行了實驗對比。實驗結果表明:牛頓法的收斂速度快于割線法,割線法快于二分法。
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈

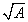 ,等價于求方程
,等價于求方程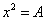 的非負根(解)。求解方程近似根的方法中,最直觀、最簡單的方法是二分法。“二分法”算法步驟如下:
的非負根(解)。求解方程近似根的方法中,最直觀、最簡單的方法是二分法。“二分法”算法步驟如下:
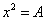 ,首先要找到一個區間 [a, b],使得f(a),f(b)異號。a可以取0,這很容易想到;但b如何選取,即如何選取b=f(A),使得
,首先要找到一個區間 [a, b],使得f(a),f(b)異號。a可以取0,這很容易想到;但b如何選取,即如何選取b=f(A),使得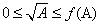 ?
?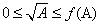 :
:
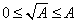 。若用A作為第一步的上界,則在A小于1時,將無法得到正確結果。
。若用A作為第一步的上界,則在A小于1時,將無法得到正確結果。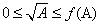 。
。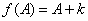 ,使得
,使得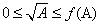 成立。
成立。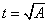 ,則t>=0,
,則t>=0,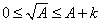 , 等價于
, 等價于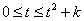 ,即
,即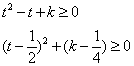
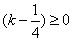 時,上式成立,所以k可以取[1/4, +∞)的任意值,不妨取k=1/4,即有
時,上式成立,所以k可以取[1/4, +∞)的任意值,不妨取k=1/4,即有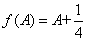 ,使得
,使得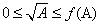 成立。
成立。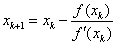

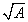 即求
即求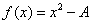 的非負根,
的非負根,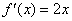 ,
,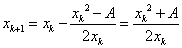
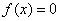 改寫成
改寫成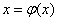 的形式;再用迭代格式
的形式;再用迭代格式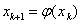 ,逐次逼近
,逐次逼近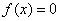 的實際解x*。
的實際解x*。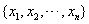 (迭代序列),數列的遞推式即
(迭代序列),數列的遞推式即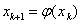 ;
;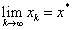
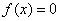 的實際解。
的實際解。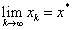 ,這很好理解;但要用此式驗證迭代式是否收斂,必須先通過遞推式
,這很好理解;但要用此式驗證迭代式是否收斂,必須先通過遞推式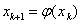 求出通項
求出通項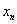 ;
;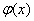 滿足:
滿足: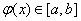 ;
;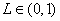 ,使得
,使得 ;
;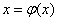 有唯一根x*;
有唯一根x*;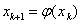 收斂,且
收斂,且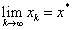 ;
;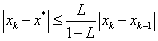 ,(事后誤差估計);
,(事后誤差估計);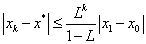 ,(事前誤差估計);
,(事前誤差估計);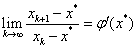
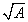 的近似解為例,說明定理如何用:
的近似解為例,說明定理如何用: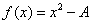 對應的迭代函數為:
對應的迭代函數為: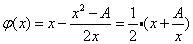
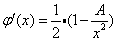
 ;
;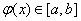 ;即滿足收斂的三個條件;
;即滿足收斂的三個條件;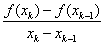
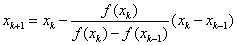

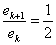 ,
,